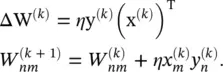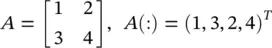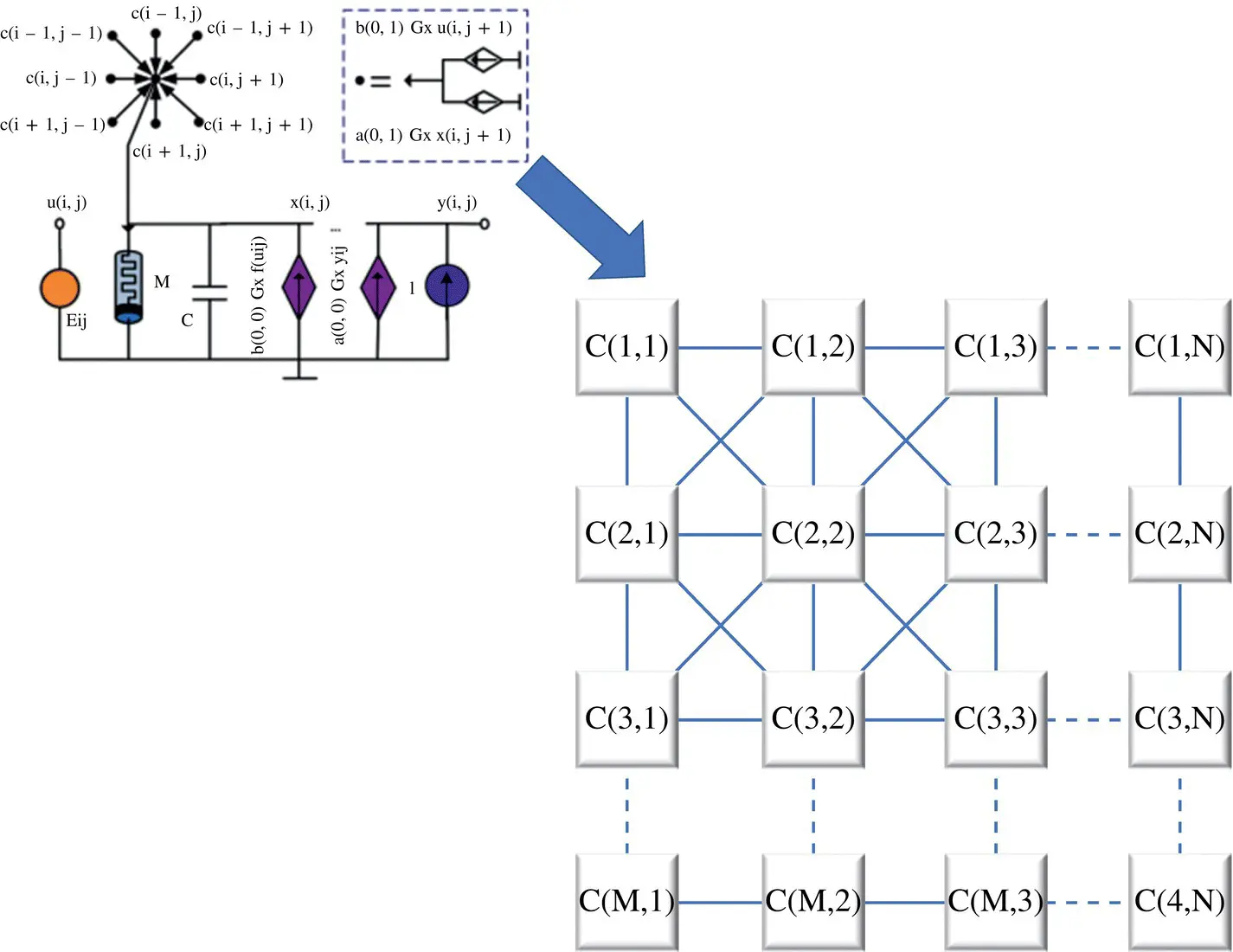
Figure 3.22 Memristor‐based cellular nonlinear/neural network (MCeNN).
Online gradient descent learning , which was described earlier, can be used here as well. With the notation used here, we assume a learning system that operates on K discrete presentations of inputs (trials), indexed by k = 1, 2, … , K . For brevity, the iteration number is sometimes not indexed when it is clear from the context. On each trial k , the system receives empirical data, a pair of two real column vector s of sizes M and N : a pattern x (k)∈ ℝ M; and a desired label d (k)∈ ℝ N, with all pairs sharing the same desired relation d (k)= f(x (k)). Note that two distinct patterns can have the same label. The objective of the system is to estimate (learn) the function f(·) using the empirical data. As a simple example, suppose W is a tunable N × M matrix of parameters, and consider the estimator
(3.75) 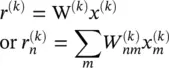
which is a single‐layer NN. The result of the estimator r = Wx should aim to predict the correct desired labels d = f ( x ) for new unseen patterns x . As before, to solve this problem, W is tuned to minimize some measure of error between the estimated and desired labels, over a K 0‐long subset of the training set (for which k = 1, … , K 0). If we define the error vector as y (k)Δ= d (k)− r (k), then a common measure is the mean square error: MSE 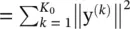 . Other error measures can be also be used. The performance of the resulting estimator is then tested over a different subset called the test set ( k = K 0+ 1, … , K ).
. Other error measures can be also be used. The performance of the resulting estimator is then tested over a different subset called the test set ( k = K 0+ 1, … , K ).
As before, a reasonable iterative algorithm for minimizing this objective is the online gradient descent ( SGD ) iteration 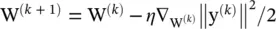 , where the 1/2 coefficient is written for mathematical convenience, η is the learning rate , a (usually small) positive constant; and at each iteration k , a single empirical sample x (k)is chosen randomly and presented at the input of the system. Using
, where the 1/2 coefficient is written for mathematical convenience, η is the learning rate , a (usually small) positive constant; and at each iteration k , a single empirical sample x (k)is chosen randomly and presented at the input of the system. Using 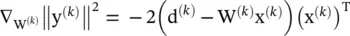 and defining Δ W (k)= W (k + 1)− W (k)and (·) Tto be the transpose operation, we obtain the outer product
and defining Δ W (k)= W (k + 1)− W (k)and (·) Tto be the transpose operation, we obtain the outer product
(3.76) 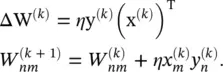
The parameters of more complicated estimators can also be similarly tuned (trained), using backpropagation, as discussed earlier in this chapter.
3.6 Convolutional Neural Network (CoNN)
Notations: In the following, we will use x ∈ ℝ Dto represent a column vector with D elements and a capital letter to denote a matrix X ∈ ℝ H × Wwith H rows and W columns. The vector x can also be viewed as a matrix with 1 column and D rows. These concepts can be generalized to higher‐order matrices, that is, tensors. For example, x ∈ ℝ H × W × Dis an order‐3 (or third‐order) tensor. It contains HWD elements, each of which can be indexed by an index triplet ( i , j , d ), with 0 ≤ i < H , 0 ≤ j < W , and 0 ≤ d < D . Another way to view an order‐3 tensor is to treat it as containing D channels of matrices.
For example, a color image is an order‐3 tensor. An image with H rows and W columns is a tensor of size H × W × 3; if a color image is stored in the RGB format, it has three channels (for R, G and B, respectively), and each channel is an H × W matrix (second‐order tensor) that contains the R (or G, or B) values of all pixels.
It is beneficial to represent images (or other types of raw data) as a tensor. In early computer vision and pattern recognition, a color image (which is an order‐3 tensor) is often converted to the grayscale version (which is a matrix) because we know how to handle matrices much better than tensors. The color information is lost during this conversion. But color is very important in various image‐ or video‐based learning and recognition problems, and we do want to process color information in a principled way, for example, as in CoNNs.
Tensors are essential in CoNN. The input, intermediate representation, and parameters in a CoNN are all tensors. Tensors with order higher than 3 are also widely used in a CoNN. For example, we will soon see that the convolution kernels in a convolution layer of a CoNN form an order‐4 tensor.
Given a tensor, we can arrange all the numbers inside it into a long vector, following a prespecified order. For example, in MATLAB, the (:) operator converts a matrix into a column vector in the column‐first order as
(3.77) 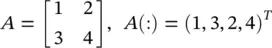
We use the notation “ vec ” to represent this vectorization operator. That is, vec ( A ) = (1, 3, 2, 4) Tin the example. In order to vectorize an order‐3 tensor, we could vectorize its first channel (which is a matrix, and we already know how to vectorize it), then the second channel, … , and so on, until all channels are vectorized. The vectorization of the order‐3 tensor is then the concatenation of the vectorizations of all the channels in this order. The vectorization of an order‐3 tensor is a recursive process that utilizes the vectorization of order‐2 tensors. This recursive process can be applied to vectorize an order‐4 (or even higher‐order) tensor in the same manner.
Vector calculus and the chain rule: The CoNN learning process depends on vector calculus and the chain rule. Suppose z is a scalar (i.e., z ∈ ℝ ) and y ∈ ℝ His a vector. If z is a function of y , then the partial derivative of z with respect to y is defined as [ ∂z / ∂y ] i= ∂z / ∂y i. In other words, ∂z / ∂y is a vector having the same size as y , and its i ‐th element is ∂z / ∂y i. Also, note that ∂z / ∂y T= ( ∂z / ∂y ) T.
Suppose now that x ∈ ℝ Wis another vector, and y is a function of x . Then, the partial derivative of y with respect to x is defined as [ ∂y / ∂x T] ij= ∂y i/ ∂x j. This partial derivative is a H × W matrix whose entry at the intersection of the i ‐th row and j ‐th column is y i/ ∂x j.
Читать дальше


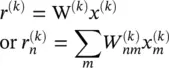
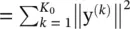 . Other error measures can be also be used. The performance of the resulting estimator is then tested over a different subset called the test set ( k = K 0+ 1, … , K ).
. Other error measures can be also be used. The performance of the resulting estimator is then tested over a different subset called the test set ( k = K 0+ 1, … , K ).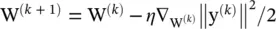 , where the 1/2 coefficient is written for mathematical convenience, η is the learning rate , a (usually small) positive constant; and at each iteration k , a single empirical sample x (k)is chosen randomly and presented at the input of the system. Using
, where the 1/2 coefficient is written for mathematical convenience, η is the learning rate , a (usually small) positive constant; and at each iteration k , a single empirical sample x (k)is chosen randomly and presented at the input of the system. Using 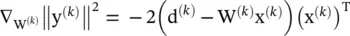 and defining Δ W (k)= W (k + 1)− W (k)and (·) Tto be the transpose operation, we obtain the outer product
and defining Δ W (k)= W (k + 1)− W (k)and (·) Tto be the transpose operation, we obtain the outer product