1 ...6 7 8 10 11 12 ...35  In math beyond arithmetic, using parentheses without another operator stands for multiplication. The parentheses can enclose the first number, the second number, or both numbers. For example,
In math beyond arithmetic, using parentheses without another operator stands for multiplication. The parentheses can enclose the first number, the second number, or both numbers. For example,

This switch makes sense when you stop to consider that the letter x , which is often used in algebra, looks a lot like the multiplication sign ×. So in this book, when I start using x to discuss algebra topics in Unit 7, I also stop using × and begin using parentheses without another sign to indicate multiplication.
Doing math lickety-split: Division
The last of the Big Four operations is division. Division literally means splitting things up. For example, suppose you’re a parent on a picnic with your three children. You’ve brought along 12 pretzel sticks as snacks, and want to split them fairly so that each child gets the same number (don’t want to cause a fight, right?).
Each child gets four pretzel sticks. This problem tells you that
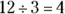
As with multiplication, division also has more than one sign: the division sign (÷) and the fraction slash (/) or fraction bar (—). So, some other ways to write the same information are
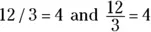
Whichever way you write it, the idea is the same: When you divide 12 pretzel sticks equally among three people, each person gets 4 of them.
 When you divide one number by another, the first number is called the dividend, the second is called the divisor, and the result is the quotient . For example, in the division from the earlier example, the dividend is 12, the divisor is 3, and the quotient is 4.
When you divide one number by another, the first number is called the dividend, the second is called the divisor, and the result is the quotient . For example, in the division from the earlier example, the dividend is 12, the divisor is 3, and the quotient is 4.
Applying the Big Four Operations to Larger Numbers
So, be honest. Are you’re feeling a bit shaky about how to apply the Big Four operations to larger numbers, especially long division? If so, don’t worry. Just use this section as a handy reference for remembering how to do stacked addition, subtraction, and multiplication, as well as everybody’s favorite, long division.
Calculating stacked addition
Stacked addition allows you to add large numbers in a systematic way.
For example, to add 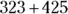 , stack the numbers up in a column format as follows:
, stack the numbers up in a column format as follows:

Next, starting in the ones’ column and working from right to left, add the numbers and place each result below the line:
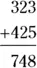
Thus, 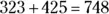 .
.
In most cases when you add, the calculation will involve carrying at least one digit from one column to the next.
For example, suppose you want to add 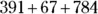 . Begin by adding
. Begin by adding 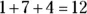 in the ones’ column, then write the 2 below the line and carry the 1 to the next column:
in the ones’ column, then write the 2 below the line and carry the 1 to the next column:
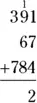
Next, add 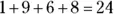 in the tens’ column, then write the 4 below the line and carry the 2:
in the tens’ column, then write the 4 below the line and carry the 2:
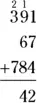
To complete the problem, add 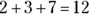 :
:
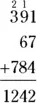
Therefore, 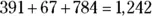 .
.
Performing stacked subtraction
As with addition, stacked subtraction allows you to subtract larger numbers systematically.
For example, to subtract 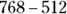 , stack the numbers as follows:
, stack the numbers as follows:
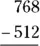
Now, as with addition, start in the ones’ column and work right to left, this time subtracting each pair of numbers in the column, and place each result below the line:
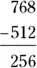
So 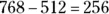 .
.
In most cases when you subtract, the calculation will involve borrowing at least one digit from one column to the next.
For example, suppose you want to subtract  :
:
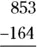
To begin, you want to subtract  in the ones’ column. However, 3 is less than 4, so to subtract, you need to borrow 1 from the tens’ column, changing the 5 to 4. Then, this 1 that you borrowed is worth 10 in the ones’ column, so add it to the 3, changing it to 13:
in the ones’ column. However, 3 is less than 4, so to subtract, you need to borrow 1 from the tens’ column, changing the 5 to 4. Then, this 1 that you borrowed is worth 10 in the ones’ column, so add it to the 3, changing it to 13:
Читать дальше

 In math beyond arithmetic, using parentheses without another operator stands for multiplication. The parentheses can enclose the first number, the second number, or both numbers. For example,
In math beyond arithmetic, using parentheses without another operator stands for multiplication. The parentheses can enclose the first number, the second number, or both numbers. For example,
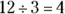
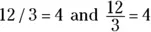
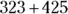 , stack the numbers up in a column format as follows:
, stack the numbers up in a column format as follows:
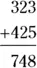
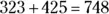 .
.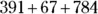 . Begin by adding
. Begin by adding 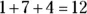 in the ones’ column, then write the 2 below the line and carry the 1 to the next column:
in the ones’ column, then write the 2 below the line and carry the 1 to the next column: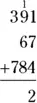
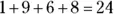 in the tens’ column, then write the 4 below the line and carry the 2:
in the tens’ column, then write the 4 below the line and carry the 2: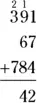
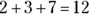 :
: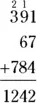
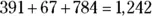 .
.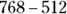 , stack the numbers as follows:
, stack the numbers as follows: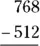
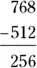
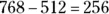 .
. :
: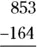
 in the ones’ column. However, 3 is less than 4, so to subtract, you need to borrow 1 from the tens’ column, changing the 5 to 4. Then, this 1 that you borrowed is worth 10 in the ones’ column, so add it to the 3, changing it to 13:
in the ones’ column. However, 3 is less than 4, so to subtract, you need to borrow 1 from the tens’ column, changing the 5 to 4. Then, this 1 that you borrowed is worth 10 in the ones’ column, so add it to the 3, changing it to 13:










