
As you can see, the notation 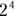 means multiply 2 by itself 4 times.
means multiply 2 by itself 4 times.
You can use exponents on numbers other than 2. Here’s another sequence you may be familiar with:
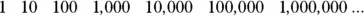
In this sequence, every number is 10 times greater than the number before it. You can also generate these numbers using exponents:
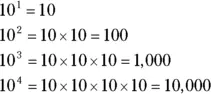
 This sequence is important for defining place value, the basis of the decimal number system, which I discuss in Chapter 3. It also shows up when I discuss decimals in Chapter 13and scientific notation in Chapter 17. You find out more about exponents in Chapter 5.
This sequence is important for defining place value, the basis of the decimal number system, which I discuss in Chapter 3. It also shows up when I discuss decimals in Chapter 13and scientific notation in Chapter 17. You find out more about exponents in Chapter 5.
Four Important Sets of Numbers
In the preceding section, you see how a variety of number sequences extend infinitely. In this section, I provide a quick tour of how numbers fit together as a set of nested systems, one inside the other.
 When I talk about a set of numbers, I’m really just talking about a group of numbers. You can use the number line to deal with four important sets of numbers.
When I talk about a set of numbers, I’m really just talking about a group of numbers. You can use the number line to deal with four important sets of numbers.
Counting numbers (also called natural numbers): The set of numbers beginning 1, 2, 3, 4 and going on infinitely
Integers: The set of counting numbers, zero, and negative counting numbers
Rational numbers: The set of integers and fractions
Real numbers: The set of rational and irrational numbers
The sets of counting numbers, integers, rational, and real numbers are nested, one inside another. This nesting of one set inside another is similar to the way that a city (for example, Boston) is inside a state (Massachusetts), which is inside a country (the United States), which is inside a continent (North America). The set of counting numbers is inside the set of integers, which is inside the set of rational numbers, which is inside the set of real numbers.
Counting on the counting numbers
The set of counting numbers is the set of numbers you first count with, starting with 1. Because they seem to arise naturally from observing the world, they’re also called the natural numbers:
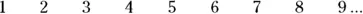
The counting numbers are infinite, which means they go on forever.
 When you add two counting numbers, the answer is always another counting number. Similarly, when you multiply two counting numbers, the answer is always a counting number. Another way of saying this is that the set of counting numbers is closed under both addition and multiplication.
When you add two counting numbers, the answer is always another counting number. Similarly, when you multiply two counting numbers, the answer is always a counting number. Another way of saying this is that the set of counting numbers is closed under both addition and multiplication.
The set of integers arises when you try to subtract a larger number from a smaller one. For example, 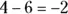 . The set of integers includes the following:
. The set of integers includes the following:
The counting numbers
Zero
The negative counting numbers
Here’s a partial list of the integers:

Like the counting numbers, the integers are closed under addition and multiplication. Similarly, when you subtract one integer from another, the answer is always an integer. That is, the integers are also closed under subtraction.
Here’s the set of rational numbers:
Integers (which include the counting numbers, zero, and the negative counting numbers)
Fractions
Like the integers, the rational numbers are closed under addition, subtraction, and multiplication. Furthermore, when you divide one rational number by another, the answer is always a rational number. Another way to say this is that the rational numbers are closed under division.
Even if you filled in all the rational numbers, you’d still have points left unlabeled on the number line. These points are the irrational numbers.
An irrational number is a number that’s neither a whole number nor a fraction. In fact, an irrational number can only be approximated as a non-repeating decimal. In other words, no matter how many decimal places you write down, you can always write down more; furthermore, the digits in this decimal never become repetitive or fall into any pattern. (For more on repeating decimals, see Chapter 13.)
The most famous irrational number is π (you find out more about π when I discuss the geometry of circles in Chapter 19):
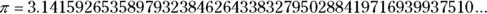
Together, the rational and irrational numbers make up the real numbers, which comprise every point on the number line. In this book, I don’t spend too much time on irrational numbers, but just remember that they’re there for future reference.
Chapter 2
IN THIS CHAPTER
 Identifying the Big Four operations (addition, subtraction, multiplication, and division)
Identifying the Big Four operations (addition, subtraction, multiplication, and division)
 Adding larger numbers with and without carrying
Adding larger numbers with and without carrying
 Subtracting larger numbers with and without borrowing
Subtracting larger numbers with and without borrowing
 Multiplying with one-digit and multiple-digit multipliers
Multiplying with one-digit and multiple-digit multipliers
 Knowing how to do long division step by step
Knowing how to do long division step by step
The operations of addition, subtraction, multiplication, and division are at the heart of arithmetic. I call them the Big Four operations.
Читать дальше


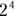 means multiply 2 by itself 4 times.
means multiply 2 by itself 4 times.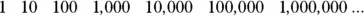
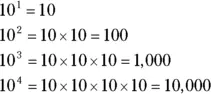
 This sequence is important for defining place value, the basis of the decimal number system, which I discuss in Chapter 3. It also shows up when I discuss decimals in Chapter 13and scientific notation in Chapter 17. You find out more about exponents in Chapter 5.
This sequence is important for defining place value, the basis of the decimal number system, which I discuss in Chapter 3. It also shows up when I discuss decimals in Chapter 13and scientific notation in Chapter 17. You find out more about exponents in Chapter 5. When I talk about a set of numbers, I’m really just talking about a group of numbers. You can use the number line to deal with four important sets of numbers.
When I talk about a set of numbers, I’m really just talking about a group of numbers. You can use the number line to deal with four important sets of numbers.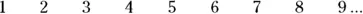
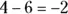 . The set of integers includes the following:
. The set of integers includes the following:
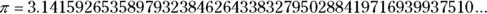
 Identifying the Big Four operations (addition, subtraction, multiplication, and division)
Identifying the Big Four operations (addition, subtraction, multiplication, and division)










