1 ...8 9 10 12 13 14 ...35 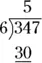
To complete this step, subtract 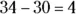 and bring down the 7 next to this result:
and bring down the 7 next to this result:
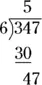
At this point, you have a new number to try dividing 6 into: 6 goes into 47 no more than 7 times. Now, multiply 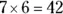 :
:
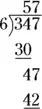
To finish up the problem, subtract 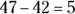 :
:
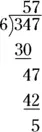
Thus, 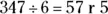 — that is, 57 with a remainder of 5.
— that is, 57 with a remainder of 5.
As another example, suppose you want to divide  . Set up the problem as follows:
. Set up the problem as follows:

To begin, note that you can divide 1,006 into 7,458 a maximum of 7 times. Thus, write 7 above the 8, multiply 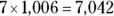 , then subtract and bring down the 5:
, then subtract and bring down the 5:

Now, you can divide 1,006 into 4,165 a maximum of 4 times. So write 4 above the line after the 7, multiply 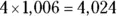 , then subtract and bring down the 3:
, then subtract and bring down the 3:

To finish the problem, you can divide 1,006 into 1,413 just 1 time. So this time, write 1 above the line after the 4, multiply 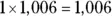 , and subtract:
, and subtract:

Therefore, 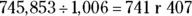 — that is, 741 with a remainder of 407.
— that is, 741 with a remainder of 407.
Unit 2
The Big Four Operations: Addition, Subtraction, Multiplication, and Division
In This Unit …
1 Chapter 3: Counting on Success: Numbers and Digits Knowing Your Place Value Close Enough for Rock ‘n’ Roll: Rounding and Estimating Practice Questions Answers and Explanations Whaddya Know? Chapter 3 Quiz Answers to Chapter 3 Quiz
2 Chapter 4: Staying Positive with Negative Numbers Understanding Where Negative Numbers Come From Sign-Switching: Understanding Negation and Absolute Value Addition and Subtraction with Negative Numbers Knowing Signs of the Times (and Division) for Negative Numbers Practice Questions Answers and Explanations Whaddya Know? Chapter 4 Quiz Answers to Chapter 4 Quiz
3 Chapter 5: Putting the Big Four Operations to Work Switching Things Up with Inverse Operations and the Commutative Property Getting with the In-Group: Parentheses and the Associative Property Understanding Inequalities Moving Beyond the Big Four: Exponents and Square Roots Practice Questions Answers and Explanations Whaddya Know? Chapter 5 Quiz Answers to Chapter 5 Quiz
Chapter 3
Counting on Success: Numbers and Digits
IN THIS CHAPTER
 Understanding how place value turns digits into numbers
Understanding how place value turns digits into numbers
 Distinguishing whether zeros are important placeholders or meaningless leading zeros
Distinguishing whether zeros are important placeholders or meaningless leading zeros
 Reading and writing long numbers
Reading and writing long numbers
 Understanding how to round numbers and estimate values
Understanding how to round numbers and estimate values
When you’re counting, ten seems to be a natural stopping point — a nice, round number. The fact that our ten fingers match up so nicely with numbers may seem like a happy accident. But of course, it’s no accident at all. Fingers were the first calculator that humans possessed. Our number system — the Hindu-Arabic numbers, also called the decimal numbers — is based on the number ten because humans have 10 fingers instead of 8 or 12. In fact, the very word digit has two meanings: numerical symbol and finger.
In this chapter, I show you how place value turns digits into numbers. I also show you when 0 is an important placeholder in a number and why leading zeros don’t change the value of a number. And I show you how to read and write long numbers. After that, I discuss two important skills: rounding numbers and estimating values.
TELLING THE DIFFERENCE BETWEEN NUMBERS AND DIGITS
Sometimes people confuse numbers and digits. For the record, here’s the difference:
A digit is a single numerical symbol, from 0 to 9.
A number is a string of one or more digits.
For example, 7 is both a digit and a number. In fact, it’s a one-digit number. However, 15 is a string of two digits, so it’s a number — a two-digit number. And 426 is a three-digit number. You get the idea.
In a sense, a digit is like a letter of the alphabet. By themselves, the uses of 26 letters, A through Z, are limited. (How much can you do with a single letter such as K or W?) Only when you begin using strings of letters as building blocks to spell words does the power of letters become apparent. Similarly, the ten digits, 0 through 9, have limited usefulness until you begin building strings of digits — that is, numbers.
Читать дальше

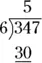
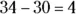 and bring down the 7 next to this result:
and bring down the 7 next to this result: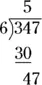
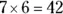 :
: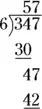
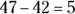 :
: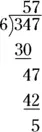
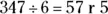 — that is, 57 with a remainder of 5.
— that is, 57 with a remainder of 5. . Set up the problem as follows:
. Set up the problem as follows:
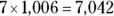 , then subtract and bring down the 5:
, then subtract and bring down the 5:
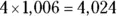 , then subtract and bring down the 3:
, then subtract and bring down the 3:
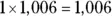 , and subtract:
, and subtract:
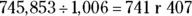 — that is, 741 with a remainder of 407.
— that is, 741 with a remainder of 407. Understanding how place value turns digits into numbers
Understanding how place value turns digits into numbers










