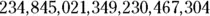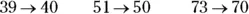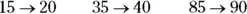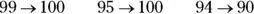The number system you’re most familiar with — Hindu-Arabic numbers — has ten familiar digits:

Yet with only ten digits, you can express numbers as high as you care to go. In this section, I show you how it happens.
Counting to ten and beyond
The ten digits in our number system allow you to count from 0 to 9. All higher numbers are produced using place value. Place value assigns a digit a greater or lesser value, depending on where it appears in a number. Each place in a number is ten times greater than the place to its immediate right.
To understand how a whole number gets its value, suppose you write the number 45,019 all the way to the right in Table 3-1, one digit per cell, and add up the numbers you get.
Table 3-145,019 Displayed in a Place-Value Chart
| Millions |
|
|
Thousands |
|
|
Ones |
|
|
| Hundred Millions |
Ten Millions |
Millions |
Hundred Thousands |
Ten Thousands |
Thousands |
Hundreds |
Tens |
Ones |
|
|
|
|
4 |
5 |
0 |
1 |
9 |
You have 4 ten thousands, 5 thousands, 0 hundreds, 1 ten, and 9 ones. The chart shows you that the number breaks down as follows:
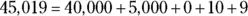
In this example, notice that the presence of the digit 0 in the hundreds place means that zero hundreds are added to the number.
Telling placeholders from leading zeros
Although the digit 0 adds no value to a number, it acts as a placeholder to keep the other digits in their proper places. For example, the number 5,001,000 breaks down into 5,000,000 + 1,000. Suppose, however, you decide to leave all the 0s out of the chart. Table 3-2shows what you’d get.
Table 3-25,001,000 Displayed Incorrectly without Placeholding Zeros
| Millions |
|
|
Thousands |
|
|
Ones |
|
|
| Hundred Millions |
Ten Millions |
Millions |
Hundred Thousands |
Ten Thousands |
Thousands |
Hundreds |
Tens |
Ones |
|
|
|
|
|
|
|
5 |
1 |
The chart tells you that 5,001,000 = 50 + 1. Clearly, this answer is wrong!
 As a rule, when a 0 appears to the right of at least one digit other than 0, it’s a placeholder. Placeholding zeros are important — always include them when you write a number. However, when a 0 appears to the left of every digit other than 0, it’s a leading zero. Leading zeros serve no purpose in a number, so dropping them is customary. For example, place the number 003,040,070 on the chart (see Table 3-3).
As a rule, when a 0 appears to the right of at least one digit other than 0, it’s a placeholder. Placeholding zeros are important — always include them when you write a number. However, when a 0 appears to the left of every digit other than 0, it’s a leading zero. Leading zeros serve no purpose in a number, so dropping them is customary. For example, place the number 003,040,070 on the chart (see Table 3-3).
Table 3-33,040,070 Displayed with Two Leading Zeros
| Millions |
|
|
Thousands |
|
|
Ones |
|
|
| Hundred Millions |
Ten Millions |
Millions |
Hundred Thousands |
Ten Thousands |
Thousands |
Hundreds |
Tens |
Ones |
| 0 |
0 |
3 |
0 |
4 |
0 |
0 |
7 |
0 |
The first two 0s in the number are leading zeros because they appear to the left of the 3. You can drop these 0s from the number, leaving you with 3,040,070. The remaining 0s are all to the right of the 3, so they’re placeholders — be sure to write them in.
When you write a long number, you use commas to separate groups of three numbers. For example, here’s about as long a number as you’ll ever see:
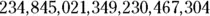
Table 3-4shows a larger version of the place-value chart.
Table 3-4A Place-Value Chart Separated by Commas
| Quintillions |
Quadrillions |
Trillions |
Billions |
Millions |
Thousands |
Ones |
| 234 |
845 |
021 |
349 |
230 |
467 |
304 |
This version of the chart helps you read the number. Begin all the way to the left and read, “Two hundred thirty-four quintillion, eight hundred forty-five quadrillion, twenty-one trillion, three hundred forty-nine billion, two hundred thirty million, four hundred sixty-seven thousand, three hundred four.”
 When you read and write whole numbers, don’t say the word and. In math, the word and means you have a decimal point. That’s why, when you write a check (does anyone still write checks?), you save the word and for the number of cents, which is usually expressed as a decimal or sometimes as a fraction. (I discuss decimals in Chapter 13.)
When you read and write whole numbers, don’t say the word and. In math, the word and means you have a decimal point. That’s why, when you write a check (does anyone still write checks?), you save the word and for the number of cents, which is usually expressed as a decimal or sometimes as a fraction. (I discuss decimals in Chapter 13.)
Close Enough for Rock ‘n’ Roll: Rounding and Estimating
As numbers get longer, calculations become tedious, and you’re more likely to make a mistake or just give up. When you’re working with long numbers, simplifying your work by rounding numbers and estimating values is sometimes helpful.
When you round a number, you change some of its digits to placeholding zeros. And when you estimate a value, you work with rounded numbers to find an approximate answer to a problem. In this section, you build both skills.
Rounding numbers makes long numbers easier to work with. In this section, I show you how to round numbers to the nearest ten, hundred, thousand, and beyond.
Rounding numbers to the nearest ten
The simplest kind of rounding you can do is with two-digit numbers. When you round a two-digit number to the nearest ten, you simply bring it up or down to the nearest number that ends in 0. For example:
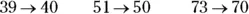
Even though numbers ending in 5 are in the middle, always round them up to the next-highest number that ends in 0:
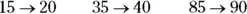
Numbers in the upper 90s get rounded up to 100:
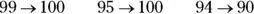
When you know how to round a two-digit number, you can round just about any number. For example, to round most longer numbers to the nearest ten, just focus on the ones and tens digits:
Читать дальше


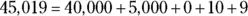
 As a rule, when a 0 appears to the right of at least one digit other than 0, it’s a placeholder. Placeholding zeros are important — always include them when you write a number. However, when a 0 appears to the left of every digit other than 0, it’s a leading zero. Leading zeros serve no purpose in a number, so dropping them is customary. For example, place the number 003,040,070 on the chart (see Table 3-3).
As a rule, when a 0 appears to the right of at least one digit other than 0, it’s a placeholder. Placeholding zeros are important — always include them when you write a number. However, when a 0 appears to the left of every digit other than 0, it’s a leading zero. Leading zeros serve no purpose in a number, so dropping them is customary. For example, place the number 003,040,070 on the chart (see Table 3-3).