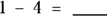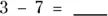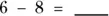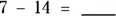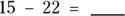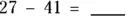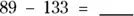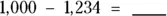Chapter 4
Staying Positive with Negative Numbers
IN THIS CHAPTER
 Working with the Big Four operations (addition, subtraction, multiplication, and division)
Working with the Big Four operations (addition, subtraction, multiplication, and division)
 Identifying which operations are inverses of each other
Identifying which operations are inverses of each other
 Knowing the operations that are commutative, associative, and distributive
Knowing the operations that are commutative, associative, and distributive
 Performing the Big Four operations on negative numbers
Performing the Big Four operations on negative numbers
 Using four symbols for inequality
Using four symbols for inequality
 Understanding exponents, roots, and absolute values
Understanding exponents, roots, and absolute values
In this chapter, you work with negative numbers — that is, numbers that are less than zero. To begin, you see how negative numbers arise when you subtract a smaller number minus a greater one. Next, you discover how to negate a number by flipping its sign. You also work with absolute value, which is the positive value of a number.
When you’re comfortable working with negative numbers, you begin to use them with the Big Four operations — addition, subtraction, multiplication, and division.
Understanding Where Negative Numbers Come From
When you first discovered subtraction, you were probably told that you can’t take a small number minus a greater number. For example, if you start with four marbles, you can’t subtract six because you can’t take away more marbles than you have. This rule is true for marbles, but in other situations, you can subtract a big number from a small one.
In real-world applications, negative numbers can represent debt. For example, if you have only five chairs to sell but a customer pays for eight of them, you owe them three more chairs. Even though you may have trouble picturing −3 chairs, you still need to account for this debt, and negative numbers are the right tool for the job.
As another example, if you have $4 and you buy something that costs $6, you end up with less than $0 dollars — that is, −$2, which means a debt of $2.
A number with a negative sign in front of it, like −2, is called a negative number. You call the number −2 either negative two or minus two. Negative numbers appear on the number line to the left of 0, as shown in Figure 4-1.

FIGURE 4-1:Negative numbers on the number line.
 When you don’t have a number line to work with, here’s a simple rule for subtracting a large number from a small number: Switch the two numbers around and take the small number from large number; then attach a negative sign to the result.
When you don’t have a number line to work with, here’s a simple rule for subtracting a large number from a small number: Switch the two numbers around and take the small number from large number; then attach a negative sign to the result.
 Q.Use the number line to subtract 5 − 8.
Q.Use the number line to subtract 5 − 8.
A. −3.On the number line, 5 − 8 means

Q.What is 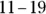 ?
?
A. −8.Because 11 is less than 19, subtract 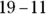 , which equals 8, and attach a negative sign to the result. Therefore,
, which equals 8, and attach a negative sign to the result. Therefore,  .
.
1  Using the number line, subtract the following numbers:
Using the number line, subtract the following numbers:
(a) 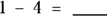
(b) 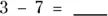
(c) 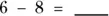
(d) 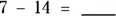
2 Find the answers to the following subtraction problems:
(a) 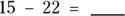
(b) 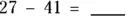
(c) 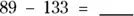
(d) 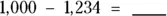
Sign-Switching: Understanding Negation and Absolute Value
 When you attach a negative sign to any number, you negate that number. Negating a number means changing its sign to the opposite sign, so
When you attach a negative sign to any number, you negate that number. Negating a number means changing its sign to the opposite sign, so
Attaching a negative sign to a positive number makes it negative.
Attaching a negative sign to a negative number makes it positive. The two adjacent (side-by-side) negative signs cancel each other out.
Attaching a negative sign to 0 doesn’t change its value, so .
Читать дальше

 Working with the Big Four operations (addition, subtraction, multiplication, and division)
Working with the Big Four operations (addition, subtraction, multiplication, and division)
 When you don’t have a number line to work with, here’s a simple rule for subtracting a large number from a small number: Switch the two numbers around and take the small number from large number; then attach a negative sign to the result.
When you don’t have a number line to work with, here’s a simple rule for subtracting a large number from a small number: Switch the two numbers around and take the small number from large number; then attach a negative sign to the result. Q.Use the number line to subtract 5 − 8.
Q.Use the number line to subtract 5 − 8.
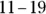 ?
?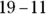 , which equals 8, and attach a negative sign to the result. Therefore,
, which equals 8, and attach a negative sign to the result. Therefore,  .
. Using the number line, subtract the following numbers:
Using the number line, subtract the following numbers: