For example, the field expression remains unchanged within the dielectric disk, while outside it is written as in Equation 2.6, with f a decaying function depending on the computation volume boundaries, Kn the modified Bessel function of the first kind and order n , and ν the radial wavenumber in the region where the EM field is radially decaying:
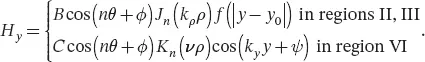 (2.6)
(2.6)
Combining the boundary conditions at the interface air/dielectric (continuity of the tangential field component) as well as the wavenumber decomposition in each region provides a set of equations describing the modes arising from the combination of a planar dielectric waveguide with a circular dielectric waveguide.
Examples of electromagnetic field maps obtained with the same method extended to the case of a ring resonator are shown in Figure 2.3. As expected from the mode description, the electric field minimum coincides with the magnetic field maximum.
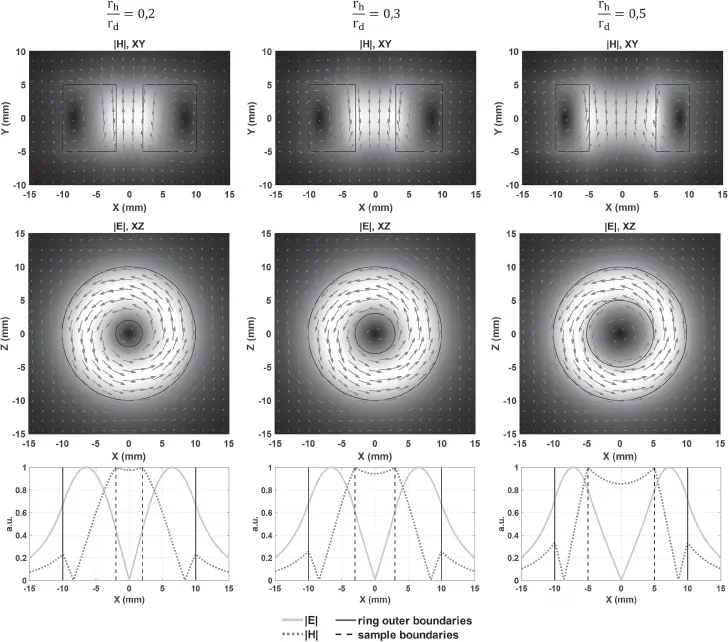
Figure 2.3 Electromagnetic field distribution of the TE 01δmode of a ring resonator (relative permittivity 500, outer radius 10 mm, height 10 mm) filled with a sample (relative permittivity 50) for varying inner to outer radii ratio: magnetic field (first line) and electric field (second line) field maps and lines (gray arrows), and both fields profiles (third line). The 2D maps are plotted in grayscale with a linear value distribution. From [21].
2.3.2 Power Loss Contributions in a Ceramic Probe
As ceramic probes do not require the use of an electronical circuit to tune and match at the Larmor frequency, the power losses are mainly due to the ceramic material losses and the electric field–sample interactions. Another contribution that is not considered here is that of the metallic feeding loop that is used to induce the mode’s field distribution in the ceramic resonator. As it is a small, nonresonant loop, its contribution is considered insignificant.
While operating in different regimes, the loss phenomenon is the same in the ceramic material and in the sample: it is energy dissipated as heat within complex permittivity materials immersed in an electromagnetic field [19]. In practice, these power losses are expressed as the integral over the object volume V of the power loss density, which involves two local variables: the imaginary part of the material permittivity and the electric field intensity. The power losses in a material of complex permittivity 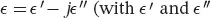 real quantities) are expressed in Equation 2.7.
real quantities) are expressed in Equation 2.7.
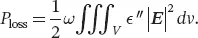 (2.7)
(2.7)
The imaginary part of the permittivity is equal to 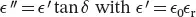 the real part of the permittivity, ϵ 0the vacuum permittivity, ϵ rthe material relative permittivity, and tan δ the total loss tangent. Materials are usually described by the quantities that can be measured in experiments, the real part of the permittivity, and the total loss tangent. The latter quantifies the effects of two distinct phenomena responsible for EM power losses in the material: bound charge polarization and electric conduction when the material has a microscopic nonzero free electron density [20]. As biological samples contain a significant proportion of water, the conductivity of the sample is dominant because of dissociated ions available in the water solution, and the losses depend on the electrical conductivity σ:
the real part of the permittivity, ϵ 0the vacuum permittivity, ϵ rthe material relative permittivity, and tan δ the total loss tangent. Materials are usually described by the quantities that can be measured in experiments, the real part of the permittivity, and the total loss tangent. The latter quantifies the effects of two distinct phenomena responsible for EM power losses in the material: bound charge polarization and electric conduction when the material has a microscopic nonzero free electron density [20]. As biological samples contain a significant proportion of water, the conductivity of the sample is dominant because of dissociated ions available in the water solution, and the losses depend on the electrical conductivity σ:
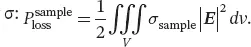
The ceramic probe is modeled as a ceramic ring resonator (inner radius r h, outer radius r d, height L , relative permittivity ϵ r, loss tangent tan δ ) filled with a cylindrical biological sample (radius r h, height L , and electrical conductivity σ sample). With the theoretical insight about the TE 01δmode field distribution provided in Section 2.3.1, it is possible, as detailed in [21], to develop an analytical expression for the power losses in the ceramic probe at the cost of some approximations:
The field distribution used to express the dielectric resonator losses is that of a lossless resonator because losses in the ceramic are considered small (tan δ ≪ 10−1).
The field distribution of the ring resonator is assumed equal to that of the corresponding disk without field leakages at the lateral boundaries.
With these assumptions, the power losses expression reduces to Equation 2.8with the axial wavenumber ky known from the mode study, 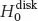 the maximum magnetic field amplitude in the disk resonator, and τ a penalty coefficient accounting for the field decreasing in the sample compared with the disk field distribution, estimated from the knowledge of both the ring and disk field distributions.
the maximum magnetic field amplitude in the disk resonator, and τ a penalty coefficient accounting for the field decreasing in the sample compared with the disk field distribution, estimated from the knowledge of both the ring and disk field distributions.
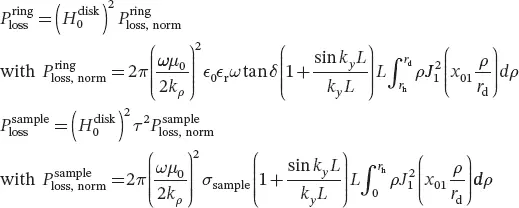 (2.8)
(2.8)
The so-called Lommel’s integrals, involving Bessel functions, can be found in [22,23].
The SNR is proportional to the transmit efficiency as follows [24]:
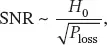 (2.9)
(2.9)
with H 0the magnetic field amplitude induced in the sample by the probe and P lossthe total power losses. For ceramic probes working with the TE 01δmode, the latter includes the ceramic resonator and the sample contributions. Assuming the magnetic field amplitude equal to that of a disk resonator in its center, weighted by the penalty coefficient τ , Equation 2.9becomes:
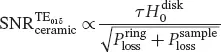
The above equation can be simplified to:
 (2.10)
(2.10)
To be used as a coil for MR imaging, the exploited mode of the resonator must be adjusted to the working frequency. In this framework estimating the mode frequency with a simple method is very useful for predesigning the ceramic probe. Methods with low computational costs provide an approximated value of the TE 01δmode frequency for disk resonators. For example, a commonly used expression, derived from simulation data, is the following:
Читать дальше

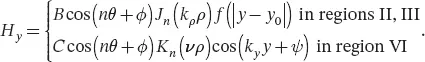 (2.6)
(2.6)
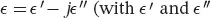 real quantities) are expressed in Equation 2.7.
real quantities) are expressed in Equation 2.7.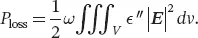 (2.7)
(2.7)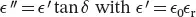 the real part of the permittivity, ϵ 0the vacuum permittivity, ϵ rthe material relative permittivity, and tan δ the total loss tangent. Materials are usually described by the quantities that can be measured in experiments, the real part of the permittivity, and the total loss tangent. The latter quantifies the effects of two distinct phenomena responsible for EM power losses in the material: bound charge polarization and electric conduction when the material has a microscopic nonzero free electron density [20]. As biological samples contain a significant proportion of water, the conductivity of the sample is dominant because of dissociated ions available in the water solution, and the losses depend on the electrical conductivity σ:
the real part of the permittivity, ϵ 0the vacuum permittivity, ϵ rthe material relative permittivity, and tan δ the total loss tangent. Materials are usually described by the quantities that can be measured in experiments, the real part of the permittivity, and the total loss tangent. The latter quantifies the effects of two distinct phenomena responsible for EM power losses in the material: bound charge polarization and electric conduction when the material has a microscopic nonzero free electron density [20]. As biological samples contain a significant proportion of water, the conductivity of the sample is dominant because of dissociated ions available in the water solution, and the losses depend on the electrical conductivity σ: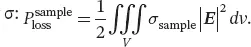
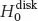 the maximum magnetic field amplitude in the disk resonator, and τ a penalty coefficient accounting for the field decreasing in the sample compared with the disk field distribution, estimated from the knowledge of both the ring and disk field distributions.
the maximum magnetic field amplitude in the disk resonator, and τ a penalty coefficient accounting for the field decreasing in the sample compared with the disk field distribution, estimated from the knowledge of both the ring and disk field distributions.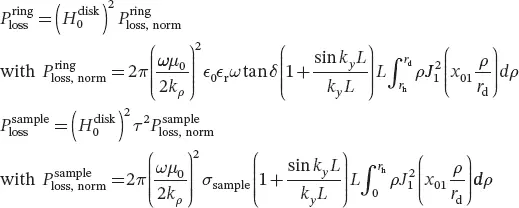 (2.8)
(2.8)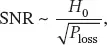 (2.9)
(2.9)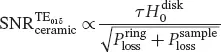
 (2.10)
(2.10)




