Richard J. Rossi - Applied Biostatistics for the Health Sciences
Здесь есть возможность читать онлайн «Richard J. Rossi - Applied Biostatistics for the Health Sciences» — ознакомительный отрывок электронной книги совершенно бесплатно, а после прочтения отрывка купить полную версию. В некоторых случаях можно слушать аудио, скачать через торрент в формате fb2 и присутствует краткое содержание. Жанр: unrecognised, на английском языке. Описание произведения, (предисловие) а так же отзывы посетителей доступны на портале библиотеки ЛибКат.
- Название:Applied Biostatistics for the Health Sciences
- Автор:
- Жанр:
- Год:неизвестен
- ISBN:нет данных
- Рейтинг книги:3 / 5. Голосов: 1
-
Избранное:Добавить в избранное
- Отзывы:
-
Ваша оценка:
- 60
- 1
- 2
- 3
- 4
- 5
Applied Biostatistics for the Health Sciences: краткое содержание, описание и аннотация
Предлагаем к чтению аннотацию, описание, краткое содержание или предисловие (зависит от того, что написал сам автор книги «Applied Biostatistics for the Health Sciences»). Если вы не нашли необходимую информацию о книге — напишите в комментариях, мы постараемся отыскать её.
APPLIED BIOSTATISTICS FOR THE HEALTH SCIENCES Applied Biostatistics for the Health Sciences
Applied Biostatistics for the Health Sciences
Applied Biostatistics for the Health Sciences — читать онлайн ознакомительный отрывок
Ниже представлен текст книги, разбитый по страницам. Система сохранения места последней прочитанной страницы, позволяет с удобством читать онлайн бесплатно книгу «Applied Biostatistics for the Health Sciences», без необходимости каждый раз заново искать на чём Вы остановились. Поставьте закладку, и сможете в любой момент перейти на страницу, на которой закончили чтение.
Интервал:
Закладка:
Probabilities are often used to determine the most likely outcome of a chance experiment and for assessing how likely it is for an observed data set to support a research hypothesis. The probability of an event A is denoted by P ( A ), and the probability of an event is always a number between 0 and 1. Probabilities near 0 indicate an event rarely occurs and probabilities near 1 indicate an event is likely to occur. Probabilities are sometimes also expressed in terms of percentages in which case the percentage is simply the probability of the event times 100. When probabilities are expressed in terms of percentages, they will be between 0 and 100%.
Example 2.19
Suppose an individual is to be drawn at random and their blood type is identified. Prior to drawing a blood sample and typing it, an individual’s blood type is unknown, and thus, this can be treated as a chance experiment. The four possible blood types are O, A, B, and AB, and hence, the sample space is S={O,A,B,AB}. Furthermore, according to the American Red Cross, the probabilities of each blood type are
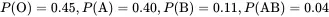
Thus, if a person is drawn at random the probability that the person will have blood type AB is 0.04.
The probabilities associated with a chance experiment and a sample space S must satisfy the following four properties known as the Axioms of Probability .
THE AXIOMS OF PROBABILITY
Probabilities are always greater than or equal to 0. That is, P(A)≥0 for any event A.
The probability of the sample space is 1. That is, P(S)=1, which means when the experiment is carried out it will result in one of the outcomes in S.
The probability of every event is between 0 and 1. That is, 0≤P(A)≤1 for every event A.
When two events have no outcomes in common, then the probability that at least one of the two events occurs is the sum of their probabilities. That is,when A and B have no outcomes in common.
Events that have no outcomes in common are called disjoint events or mutually exclusive events . If A and B are disjoint events, then the probability of the event “ A and B ” is 0. That is, it is impossible for the events to occur simultaneously.
2.3.1 Basic Probability Rules
Determining the probabilities associated with complex real-life events often requires a great deal of information and an extensive scientific understanding of the structure of the chance experiment being studied. In fact, even when the sample space and event are easily identified, the determination of the probability of an event can be an extremely difficult task. For example, in studying the side effects of a drug, the possible side effects can generally be anticipated and the sample space will be known. However, because humans react differently to drugs, the probabilities of the occurrence of the side effects are generally unknown. The probabilities of the side effects are often estimated in clinical trials.
The following basic probability rules are often useful in determining the probability of an event.
1 When the outcomes of a random experiment are equally likely to occur, the probability of an event A is the number of outcomes in A divided by the number of simple events in S. That is,
2 For every event A, the probability of A is the sum of the probabilities of the outcomes comprising A. That is, when an event A is comprised of the outcomes O1,O2,…,Ok, the probability of the event A is
3 For any two events A and B, the probability that either event A or event B occurs is
4 The probability that the event A does not occur is 1 minus the probability that the event A does occur. That is,
Example 2.20
Table 2.8gives a breakdown of the pool of 242 volunteers for a university study on rapid eye movement (REM). Use Table 2.8to determine the probability that
Table 2.8 Summary Table for the n=242 Volunteers in a University Study of Rapid Eye Movement (REM)
| Gender | Age | |||
|---|---|---|---|---|
| <18 | 18–20 | 21–25 | >25 | |
| Female | 3 | 58 | 42 | 25 |
| Male | 1 | 61 | 43 | 9 |
1 a female volunteer is selected,
2 a male volunteer younger than 21 is selected,
3 a male volunteer or a volunteer older than 25 is selected.
SolutionsLet F be the event a female volunteer is selected, M the event a male volunteer is selected, 21 the event a volunteer younger than 21 is selected, and 25 the event that a volunteer older than 25 is selected. Since a volunteer will be selected at random, each volunteer is equally likely to be selected, and thus,
1 the probability that a female volunteer is selected is
2 the probability that a male volunteer younger than 21 is selected is
3 the probability that a male volunteer or a volunteer older than 25 is selected is
Example 2.21
Use table of percentages for blood type and Rh factor given in Table 2.9to determine the probability that a randomly selected individual
Table 2.9 The Percentages of Each Blood Type and Rh Factor
| Blood Type | Rh Factor | |
|---|---|---|
| + | − | |
| O | 38% | 7% |
| A | 34% | 6% |
| B | 9% | 2% |
| AB | 3% | 1% |
1 has Rh positive blood,
2 has type A or type B blood,
3 has type A blood or Rh positive blood.
SolutionsBased on the percentages given in Table 2.9
1 Rh positive blood is O+, A+, B+, and AB+, and thus, the probability that a randomly selected individual has Rh positive blood is
2 type A or type B blood is A+, A−, B+, B−. Thus,
3 the probability an individual has type A blood or Rh positive blood is
2.3.2 Conditional Probability
In many biomedical studies, the probabilities associated with a qualitative variable will be modeled. A good probability model will take into account all of the factors believed to cause or explain the occurrence of the event. For example, the probability of survival for a melanoma patient depends on many factors including tumor thickness, tumor ulceration, gender, and age. Probabilities that are functions of a particular set of conditions are called conditional probabilities .
Conditional probabilities are simply probabilities based on well-defined subpopulations defined by a particular set of conditions (i.e., explanatory variables). The conditional probability of the event A given that the event B has occurred is denoted by P(A|B) and is defined as
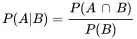
provided that P(B)≠0. Specifying that the event B has occurred places restrictions on the outcomes of the chance experiment that are possible. Thus, the outcomes in the event B become the subpopulation upon which the probability of the event A is based.
Example 2.22
Suppose that in a population of 100 units 35 units are in event A , 48 of the units are in event B , and 22 units are in both events A and B . The unconditional probability of event A is P(A)=35100=0.35. The conditional probability of event A given that event B has occurred is
Читать дальшеИнтервал:
Закладка:
Похожие книги на «Applied Biostatistics for the Health Sciences»
Представляем Вашему вниманию похожие книги на «Applied Biostatistics for the Health Sciences» списком для выбора. Мы отобрали схожую по названию и смыслу литературу в надежде предоставить читателям больше вариантов отыскать новые, интересные, ещё непрочитанные произведения.
Обсуждение, отзывы о книге «Applied Biostatistics for the Health Sciences» и просто собственные мнения читателей. Оставьте ваши комментарии, напишите, что Вы думаете о произведении, его смысле или главных героях. Укажите что конкретно понравилось, а что нет, и почему Вы так считаете.