A nucleus in a liquid experiences a fluctuating field, due to the magnetic moments of nuclei in other molecules as they undergo thermal motions. (This experience of a fluctuating field is actually true for all environments, not just a nucleus in a liquid.) This fluctuating field may be resolved by Fourier analysis into a series of terms that are oscillating at different frequencies, which may be further divided into components parallel to B 0and perpendicular to B 0. The component parallel to B 0could influence the steadiness of the static field B 0, while the components perpendicular to the static field at the Larmor frequency could induce transitions between the levels in a similar way to B 1. These influences give rise to a non-adiabatic (or non-secular) contribution to relaxation of both the longitudinal and transverse components of M.
If the fluctuating field manages to alter the populations of the states, the populations would evolve immediately until they reach the values predicted by the Boltzmann equations for the temperature of the Brownian motion (lattice temperature). This process is described by T 1and results in the relaxation of the longitudinal component of M. The contribution of the fluctuating field to T 2can be seen from the following argument. According to Eq. ( 3.9)–Eq. (3.11), the Zeeman energy levels are known precisely (Figure 3.1), which implies the resonance frequency associated with the transition between two neighboring Zeeman levels should have a unique value, that is, a delta function at a singular ω 0(Figure 3.2a). In reality, however, the resonant peak even in simple liquids is broadened due to the fluctuation of the Zeeman levels (Figure 3.2b), caused by the distributions of local interactions in their environment experienced by the nuclear spins. The line width of the resonant peak (excluding the effect of inhomogeneity in B 0), which is inversely proportional to T 2, is a measure of the uncertainty in the energies between two neighboring Zeeman levels. This uncertainty can also be traced back to the fluctuating fields due to the magnetic moments of nuclei in other molecules as they undergo thermal motions.

Figure 3.2 (a) A precise value of the Zeeman energy difference between the two states in a spin-½ system should imply a single value in the transition, hence a delta function in the frequency distribution. (b) In reality, a wider line shape such as a Lorentzian or Gaussian suggests an uncertainty in the difference between the energy levels. For simple liquids, the line shape is a Lorentzian in the frequency domain, which corresponds to the exponential decay in the time-domain FID, shown in (c). A fast decay of the FID (e.g., short blue dash) implies a short T 2and a wide line shape; a slow decay (e.g., red solid line) implies a long T 2and a narrow line shape. A precise value of the energy difference as in (a) would imply a sinusoidal oscillation without any decay in the time domain (as shown in Figure 2.15d).
The Bloch equation [Eq. (2.18)] contains a phenomenological term leading to exponential relaxation. This classical description is quite accurate for spins in rapidly tumbling molecules but breaks down when the motions of molecules become slow or complex, such as in the case of internal motion in macromolecules. In the following sections, we first explain the relaxation mechanisms in terms of quantum transitions between eigenstates of operators Ix, Iy , and Iz ; then, we briefly describe the results of the random field model of relaxation.
3.7.1 Relaxation Mechanism in Terms of Quantum Transitions
For spin-1/2 particles, the relaxation mechanism can be understood with a set of equations and analysis in terms of quantum transition [9, 10]. In this approach, the spin populations (the occupancies of the eigenstates of Iz with eigenvalues m=±1/2) are defined as
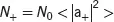 (3.25a)
(3.25a)
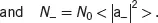 (3.25b)
(3.25b)
We also define the total population N 0and the population difference n as
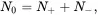 (3.26a)
(3.26a)
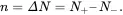 (3.26b)
(3.26b)
Hence, the macroscopic magnetization M is proportional to the population difference n . Using Eq. ( 3.21), the z component of the magnetization at time = 0 can be written as
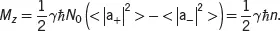 (3.27)
(3.27)
Since the population is at equilibrium with the environment according to the Boltzmann distribution, the population ratio is
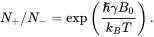 (3.28)
(3.28)
To consider the dynamics of the two populations, we define w+- as the probability of transition of a spin from |+> state to |–> state per spin per second, and w-+ as the probability of transition of a spin from |–> state to |+> state per spin per second. At equilibrium, we have
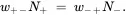 (3.29)
(3.29)
Combining Eq. ( 3.28) and Eq. ( 3.29), we have
 (3.30)
(3.30)
With this equation, the changes of the spins with time can be defined as
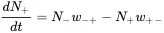 (3.31a)
(3.31a)
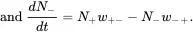 (3.31b)
(3.31b)
Each equation in Eq. (3.31) has two terms, the increment term (the first term) and the reduction term (the second term). Given the fact that w +-≈ w -+, we define
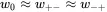 (3.32a)
(3.32a)
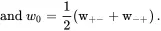 (3.32b)
(3.32b)
Note that w 0can be considered as the probability of induced transitions, while the term ℏγB0/kBT can be considered as the probability of spontaneous transitions; their differences were distinguished first by Albert Einstein in 1916 when he published a paper on different processes occurring in the formation of an atomic spectral line in optical studies. And hence we can show that
Читать дальше


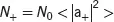 (3.25a)
(3.25a)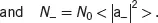 (3.25b)
(3.25b)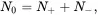 (3.26a)
(3.26a)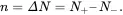 (3.26b)
(3.26b)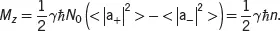 (3.27)
(3.27)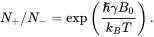 (3.28)
(3.28)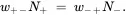 (3.29)
(3.29) (3.30)
(3.30)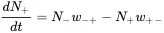 (3.31a)
(3.31a)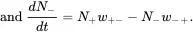 (3.31b)
(3.31b)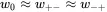 (3.32a)
(3.32a)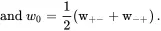 (3.32b)
(3.32b)










