Note that only the Iz component is present in the last part of Eq. ( 3.5), which is due to the properties of the dot product (cf. Appendix A1.1) since B 0= B 0 k.
As in the classical description where Iis the spin angular momentum (a vector) and the half-integer or integer values of Iare called spin quantum number I , the spin operator Iz has m possible values (the eigenvalues), ranging from − I , − I + 1, …, I , where m is the azimuthal quantum number.
Therefore, the evolution operator U ( t ) can be written as
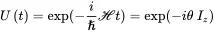 (3.6)
(3.6)
where the second step considers the fact that ω 0= γB 0and θ = ω 0 t . U ( t ) is hence just a rotation operator [recall that exp (iθ)= cosθ + i sinθ, also in Appendix A1.1], which corresponds to a rotation of the spin state |ψ> about the z axis with an angular frequency ω 0, known as the Larmor precession frequency:
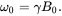 (3.7)
(3.7)
This equation is identical to the equation that we have derived in the classical description [Eq. (2.5)].
From the energy eigenvalue equation,
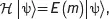 (3.8)
(3.8)
one can obtain the energy eigenvalues of the Zeeman Hamiltonian ℋ, which are the energy levels (called the Zeeman levels):
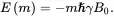 (3.9)
(3.9)
Therefore, the energy difference Δ E between any two adjacent eigenstates of a spin system, known as the Zeeman splitting, is
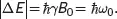 (3.10)
(3.10)
As indicated in Eq. ( 3.9), a spin-1/2 system ( I = 1/2) has only two eigenstates, corresponding to m = +1/2 (spin-up) and m = –1/2 (spin-down) states. Its two energy levels are therefore given by
 (3.11a)
(3.11a)
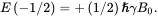 (3.11b)
(3.11b)
Schematically, these two energy levels, which were shown once before briefly in Figure 2.2a, are now shown more completely in Figure 3.1. Note that for the spin-1/2 system, the “spin-up” and “spin-down” states are stationary states of the system and exist only in a time-independent magnetic field, that is, when ℋ is time-independent. Note also that the schematic in Figure 3.1, where E (–1/2) has a higher energy than E (+1/2), is based on a positive γ .

Figure 3.1 The quantities in a spin-1/2 system. The application of an external magnetic field B 0introduces two energy levels for the spin-1/2 system. The population difference between the two states, determined by the Boltzmann distribution, results in a macroscopic magnetization, M, pointing along the same direction as the external magnetic field.
The terms “spin-up” and “spin-down” refer to the z -component mħ of the angular momentum. The actual spin vector has a magnitude of ℏI(I+1), which is greater than mħ . Hence, a spin vector Icannot lie graphically along any fixed axis in space. This is the reason that the precessional motion of a nucleus spin in a classical description is tilted at a fixed angle (Figure 2.3b). Since Ix, Iy , and Iz do not commute, we cannot specify or measure any two quantities simultaneously. Only the z -component Iz and the magnitude of Iare known with certainty as Iz = 1/2 and I 2= 3/4, which can be used to determine the fixed angle of the cone in Figure 2.3b and Figure 2.4b.
Instead of visualizing a vector µprecessing on the surface of a cone, a spin vector in the stationary state can be thought of as uniformly smeared out over the surface of a cone, similar to the advanced concept in modern physics that visualizes an electron as a cloud around a nucleus instead of a point charge in an orbit around the nucleus. In addition, quantum mechanically, a nuclear spin in a stationary state does not precess, since the probability density and expectation values are independent of time. Since Iis uniformly smeared out as described and cannot be specified to lie completely along any axis, we should only be concerned with the components of I, not Iitself. Therefore, the spin-up state can be thought of as a spin vector lying along the z axis, parallel with the field direction.
3.3 MACROSCOPIC MAGNETIZATION
Any practical sample, no matter how small, contains an enormous number of nuclei. It is the macroscopic ensemble average of the observable quantities in which we are interested. In these ensembles, different nuclei may occupy different states | ψ >. We use the concept of sub-ensemble in which all nuclei are in identical states | ψ ( t )>. The sum over all sub-ensembles, each with a classical probability p ψ, gives the observable ensemble average in which we are interested. The averaged expectation value, by definition, is
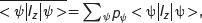 (3.12)
(3.12)
where the bar refers to the statistical ensemble average, and the pair of arrow brackets, < >, represents the quantum mechanical expectation value.
Now consider spin-1/2 particles. In NMR, the dominant interaction of a spin with its environment is always via the Zeeman interaction [as in Eq. ( 3.5)]. This means that the natural eigenstates are those whose quantum numbers are eigenvalues of Iz , that is, |1/2> and |–1/2>.
In general, we can express any state in this basis using the Pauli’s spin matrices formalism (cf. Appendix A2.5), as
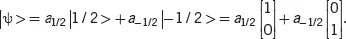 (3.13)
(3.13)
Since Iz=12[100−1], the ensemble averaged expectation value of Iz is determined by the difference in populations between the upper and lower energy levels, according to the Boltzmann distribution. This distribution describes the polarization of the ensemble in thermal equilibrium.
We can calculate the normalized population at thermal equilibrium as
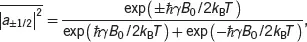 (3.14)
(3.14)
Читать дальше

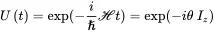 (3.6)
(3.6)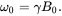 (3.7)
(3.7)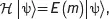 (3.8)
(3.8)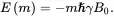 (3.9)
(3.9)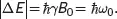 (3.10)
(3.10) (3.11a)
(3.11a)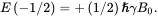 (3.11b)
(3.11b)
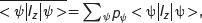 (3.12)
(3.12)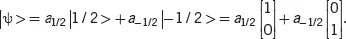 (3.13)
(3.13)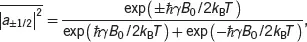 (3.14)
(3.14)










