Yang Xia - Essential Concepts in MRI

With this in mind, we can make some further comments on the laboratory and rotating frames. In the laboratory (stationary) frame, the z axis is firmly defined by the direction of B 0(as shown in Figure 1.2), while the x and y axes are commonly defined by the typical 3D Cartesian coordinates in the 2D transverse plane, which is perpendicular to the z axis (Figure 1.3). In the rotating frame, the direction of the x′ axis is quite arbitrary, defined at the instant when the B 1( t ) field is switched on. For a single B 1( t ) field, whether B 1is along the x′ or y′ or –x′ or –y′ axis does not matter at all, since the variation of the B 1direction only results in the exchange of the absorption and dispersion terms in Eq. (2.34). Even when the B 1direction is at an arbitrary angle between the x′ and y′ axes in the transverse plane, it results in only slightly complicated quadrature signals, where the mixed terms can be and are always phase-adjusted in the phasing process after the signal acquisition [with the use of a simple 2D rotation, as Eq. (A1.23)]. The phase of a B 1field/pulse becomes critical only when this pulse is among a train of B 1pulses, that is, the relative phases among the B 1pulses in a pulse train do matter.

1 1.Harris RK, Becker ED, Cabral De Menezes SM, Goodfellow R, Granger P. NMR Nomenclature. Nuclear Spin Properties and Conventions for Chemical Shifts (IUPAC Recommendations 2001). Pure Appl Chem. 2001; 73(11):1795–818.

2 2.Callaghan PT. Principles of Nuclear Magnetic Resonance Microscopy. Oxford: Oxford University Press; 1991.

3 3.Hennel JW, Klinowski J. Fundamentals of Nuclear Magnetic Resonance. Essex: Longman Scientific & Technical; 1993.

4 4.Harris RK. Nuclear Magnetic Resonance Spectroscopy – A Physicochemical View. Essex: Longman Scientific & Technical; 1983.

5 5.Bovey FA. Nuclear Magnetic Resonance Spectroscopy. 2nd ed. San Diego, CA: Academic Press; 1988.

6 6.Meadows M. Precession and Sir Joseph Larmor. Concepts in Magnetic Resonance. 1999; 11(4):239–41.

7 7.Bloch F. Nuclear Induction. Phys Rev. 1946;70(7–8):460–74.

8 8.Bracewell R. The Fourier Transform and Its Applications. New York: McGraw-Hill Book Company; 1965.

9 9.Press WH, Flannery BP, Teukolsky SA, Vetterling WT. Numerical Recipes. Cambridge: Cambridge University Press; 1989.

10 10.Hoult DI, Richards RE. The Signal-to-Noise Ratio of the Nuclear Magnetic Resonance Experiment. J Magn Reson. 1976; 24:71–85.

1 1 Larmor precession is named after Irish physicist Joseph Larmor, who in 1897 first described the circular motion of the magnetic moment of an orbiting charged object about an external magnetic field.

Although the visualization of a vector Mmoving under the direction of a B 1pulse is useful for the understanding of the simplest cases in NMR and MRI, a deep understanding of magnetic resonance [1–6] requires the aid of quantum mechanics, where the essential information of the nuclear systems is contained in the complex wave functions (labeled with Greek letters Ψ, Φ, φ , ψ). These wave functions can be described by the use of a vectoral term called a ket and written as | φ >. For each | φ >, one further defines a conjugated vector of a different nature, called a bra and written as < φ |. (The terms bra and ket come from truncations of the word bracket .)

In modern physics, the energies ( E ) and wave functions (ψ) for a molecular or atomic system can be investigated by the use of the Schrödinger equation (ℋ ψ = E ψ), where the operator ℋ is called the Hamiltonian and commonly contains the differential operator ∇2. (A spin term is usually neglected for the computation of atomic and molecular orbitals because its influence, in terms of energy shift, is negligibly small in the absence of a magnetic field.) A similar quantum mechanical equation can describe the nuclear spins where the Hamiltonian contains the spin angular momentum operator. In NMR, the stable states of quantum mechanics systems are the eigenfunctions of H. Hence, to calculate NMR spectra we must find the eigenvalues of H.

In Chapter 2, the classical description of NMR, spin angular momentum is visualized as a spinning sphere that carries a charge (Figure 2.3b). In a quantum mechanical description of NMR, spin angular momentum is a quantum mechanical quantity without a classical analog; spin angular momentum is determined by the internal nuclear structure of the spin system. A classical limit is only approached in the case of orbital angular momentum and in the limit of large quantum numbers. Appendix 2 has some background introduction in quantum mechanics. This chapter presents the quantum mechanical description of the fundamental NMR concepts.

A nuclear spin in quantum mechanical description is represented by a spin angular momentum operator I, which can be written in the usual Cartesian coordinate system as a dimensionless quantity

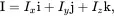(3.1)

where Ix , Iy , and Iz are the spin operators representing the x , y , z components of the spin operator I.

The magnetic moment µis proportional to its spin angular momentum,

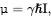(3.2)

where γ is a proportionality constant (called the gyromagnetic ratio), different for different nuclear species. This equation is identical to that in the classical description [Eq. (2.1)], except the spin Iis now an operator.

A single nucleus in an external magnetic field ( B 0= B 0 k) experiences the nuclear Zeeman interaction 1with the field. The evolution of a spin system ψ is governed by the time-dependent Schrödinger equation,

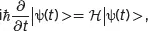(3.3)

where ℋ is a Hamiltonian. (This equation plays a similar role as Eq. (2.3) in classical treatment of NMR in Chapter 2, where the Newton’s second law was used.) If ℋ is considered time-independent, the evolution of the spin system can be derived from the above equation as

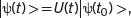(3.4)

where U ( t ) is the evolution operator. This equation effectively separates the time-independent part |ψ( t 0)> from the time-dependent part U ( t ).

Since the Hamiltonian operator for the case of B 0= B 0 kis given by the Zeeman Hamiltonian, we can write down the operator ℋ as

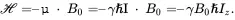(3.5)