Philip Hofmann - Solid State Physics

X‐rays interact rather weakly with matter. A description of X‐ray diffraction can therefore be restricted to single scattering, meaning that we limit our analysis to the case that X‐rays incident upon a crystal sample get scattered not more than once (most are not scattered at all). This is called the kinematic approximation;it greatly simplifies matters and is used throughout the treatment in this book. Furthermore, we will assume that the X‐ray source and detector are placed very far away from the sample so that the incoming and outgoing waves can be treated as plane waves. X‐ray diffraction of crystals was discovered and described by M. von Laue in 1912. Also in 1912, W. L. Bragg came up with an alternative description that is considerably simpler and will serve as a starting point for our analysis.

Bragg treated the problem as the reflection of the incident X‐rays at flat crystal planes. These planes could, for example, be the close‐packed planes making up fcc and hcp crystals, or they could be alternating Cs and Cl planes making up the CsCl structure. At first glance, the physical justification for this picture seems somewhat dubious, because the crystal planes appear certainly not “flat” for X‐rays with wavelengths on the order of atomic spacing. Nevertheless, the description proved highly successful, and we shall later see that it is actually a special case of the more complex Laue description of X‐ray diffraction.

Figure 1.8shows the geometrical considerations behind the Bragg description. A collimated beam of monochromatic X‐rays hits the crystal. The intensity of diffracted X‐rays is measured in the specular direction . The angles of incidence and emission are 90 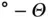. The condition for constructive interference is that the path length difference between the X‐rays reflected from one layer and the next layer is an integer multiple of the wavelength 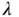. In the figure, this means that 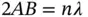, where 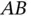is the distance between points A and B and 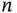is a natural number. On the other hand, we have 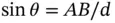, which leads us to the Bragg condition

(1.3)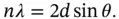

It is obvious that if this condition is fulfilled for one specific layer and the layer below it, then it will also be fulfilled for any number of layers with identical spacing. In fact, the X‐rays penetrate very deeply into the crystal so that thousands of layers contribute to the reflection. This results in very sharp maxima in the diffracted intensity, similar to the situation for an optical grating with many lines. The Bragg condition can obviously only be fulfilled for 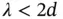, putting an upper limit on the wavelength of the X‐rays that can be used for crystal structure determination.

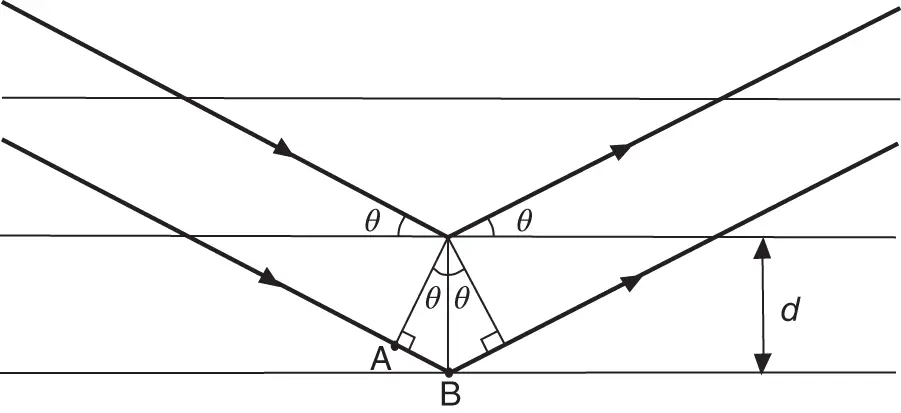
Figure 1.8 Construction for the derivation of the Bragg condition. The horizontal lines represent the crystal lattice planes that are separated by a distance 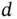. The heavy lines represent the X‐rays.

Obviously, the Bragg condition will be satisfied not only for a special kind of lattice plane in a crystal, such as the hexagonal planes in an hcp crystal, but for all possible parallel planes in a structure. Thus, we need a more precise definition of the term lattice plane. It proves useful to define a lattice plane as a plane containing at least three non‐collinear lattice points of a given Bravais lattice. If it contains three points, it will actually contain infinitely many because of the translational symmetry of the lattice. Examples for lattice planes in a simple cubic structure are shown in Figure 1.9.

Figure 1.9 Three different lattice planes in the simple cubic structure characterized by their Miller indices.

Following this definition, all lattice planes can be characterized by a set of three integers, the so‐called Miller indices. We derive them in three steps:

1 We find the intercepts of the specific plane at hand with the crystallographic axes in units of the lattice vectors, for example, for the leftmost plane in Figure 1.9.

2 We take the “reciprocal value” of these three numbers. For our example, this gives .

3 We multiply the numbers obtained in this manner with some factor so that we arrive at the smallest set of integers having the same ratio. In the example given, this is not necessary as all number are already integers.

Such a set of three integers can then be used to denote any given lattice plane. Later, we will encounter a different and more elegant definition of the Miller indices.

In practice, the X‐ray diffraction peaks are so sharp that it is difficult to align and move the sample so that the incoming and reflected X‐rays lie in a plane normal to a certain crystal plane. An elegant way to circumvent this problem is to use a powder consisting of very small crystals instead of a large single crystal. This will not only ensure that some of the many crystals are oriented correctly to get constructive interference from a certain set of crystal planes, it will also automatically yield the interference pattern for all possible crystal planes.

The Bragg theory for X‐ray diffraction is useful for extracting the distances between lattice planes in a crystal, but it has its limitations. Most importantly, it does not provide any information on what the lattice actually consists of, that is, the basis. Also, the fact that the X‐rays are described as being reflected by planes is physically somewhat obscure. In the following, we will therefore discuss a more general description of X‐ray diffraction that goes back to M. von Laue.

The physical process leading to X‐ray scattering is that the electromagnetic field of the X‐rays forces the electrons in the material to oscillate with the same frequency as that of the field. The oscillating electrons then emit new X‐rays that give rise to an interference pattern. For the following discussion, however, it is merely important that something scatters the X‐rays, not what it is.