1 ...8 9 10 12 13 14 ...22 Equation 1.11is our final result. It relates the measured intensity to the electron concentration in the sample. Except for very light elements, most of the electrons are located close to the ion cores and the electron concentration that scatters the X‐rays is essentially identical to the geometrical arrangement of the atomic cores. Hence, Eq. (1.11)can be used for the desired structure determination. To this end, one could try to measure the intensity as a function of scattering vector 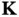 and to infer the structure from the result. This is a formidable task, however. It is greatly simplified by the fact that the specimen under investigation is a crystal with a periodic lattice. In the following, we introduce the mathematical tools and concepts that are needed to exploit the crystalline structure in the analysis. The most important of these is the so‐called reciprocal lattice.
and to infer the structure from the result. This is a formidable task, however. It is greatly simplified by the fact that the specimen under investigation is a crystal with a periodic lattice. In the following, we introduce the mathematical tools and concepts that are needed to exploit the crystalline structure in the analysis. The most important of these is the so‐called reciprocal lattice.
1.3.1.4 The Reciprocal Lattice
The concept of the reciprocal lattice is fundamental to solid state physics because it permits us to exploit crystal symmetry in the analysis of many problems. Here, we will use it to describe X‐ray diffraction from periodic structures and we will continue to meet it again in the following chapters. Unfortunately, the meaning of the reciprocal lattice turns out to be difficult to grasp. We will start out with a formal definition and provide some of its mathematical properties. We then go on to discuss the meaning of the reciprocal lattice before we come back to X‐ray diffraction. The full importance of the concept will become apparent in the course of this book.
For a given Bravais lattice
(1.12) 
we define the reciprocal lattice as the set of vectors 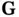 for which
for which
(1.13) 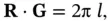
where 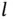 is an integer. Equivalently, we could require that
is an integer. Equivalently, we could require that
(1.14) 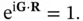
Note that this equation must hold for any choice of the lattice vector 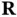 and reciprocal lattice vector
and reciprocal lattice vector 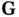 . We can write any
. We can write any 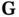 as the linear combination of three vectors
as the linear combination of three vectors
(1.15) 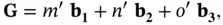
where 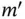 ,
, 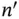 and
and 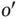 are integers. The reciprocal lattice is also a Bravais lattice. The vectors
are integers. The reciprocal lattice is also a Bravais lattice. The vectors 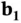 ,
, 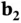 , and
, and 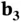 spanning the reciprocal lattice can be constructed explicitly from the lattice vectors 1
spanning the reciprocal lattice can be constructed explicitly from the lattice vectors 1
(1.16) 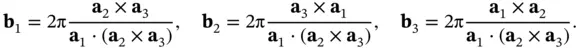
From this, one can derive the simple but useful property 2
(1.17) 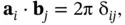
which can easily be verified. Equation (1.17)can then be used to verify that the reciprocal lattice vectors defined by Eqs. (1.15)and (1.16)do indeed fulfill the fundamental property of Eq. (1.13)defining the reciprocal lattice (see also Problem 6).
Another way to view the vectors of the reciprocal lattice is as wave vectors that yield plane waves with the periodicity of the Bravais lattice, because
(1.18) 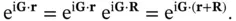
Using the reciprocal lattice, we can finally define the Miller indicesin a much simpler way: The Miller indices 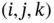 define a plane that is perpendicular to the reciprocal lattice vector
define a plane that is perpendicular to the reciprocal lattice vector 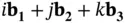 (see Problem 9).
(see Problem 9).
1.3.1.5 The Meaning of the Reciprocal Lattice
We have now defined the reciprocal lattice in a proper way, and we will give some simple examples of its usefulness. The most important feature of the reciprocal lattice is that it facilitates the description of functions with the same periodicity as that of the lattice. To see this, consider a one‐dimensional lattice, a chain of points with a lattice constant 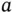 ( Fig. 1.11). We are interested in a function with the periodicity of the lattice, such as the electron concentration
( Fig. 1.11). We are interested in a function with the periodicity of the lattice, such as the electron concentration 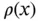 along the chain,
along the chain, 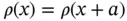 . We can write this as a Fourier series of the form
. We can write this as a Fourier series of the form
(1.19) 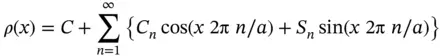
with real coefficients 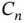 and
and 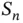 . The sum starts at
. The sum starts at 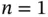 , the constant
, the constant 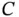 is therefore outside the summation. Using complex coefficients
is therefore outside the summation. Using complex coefficients 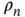 , we can also write this in the more compact form
, we can also write this in the more compact form
Читать дальше

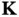 and to infer the structure from the result. This is a formidable task, however. It is greatly simplified by the fact that the specimen under investigation is a crystal with a periodic lattice. In the following, we introduce the mathematical tools and concepts that are needed to exploit the crystalline structure in the analysis. The most important of these is the so‐called reciprocal lattice.
and to infer the structure from the result. This is a formidable task, however. It is greatly simplified by the fact that the specimen under investigation is a crystal with a periodic lattice. In the following, we introduce the mathematical tools and concepts that are needed to exploit the crystalline structure in the analysis. The most important of these is the so‐called reciprocal lattice.
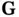 for which
for which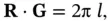
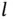 is an integer. Equivalently, we could require that
is an integer. Equivalently, we could require that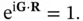
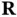 and reciprocal lattice vector
and reciprocal lattice vector 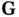 . We can write any
. We can write any 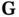 as the linear combination of three vectors
as the linear combination of three vectors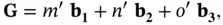
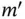 ,
, 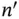 and
and 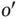 are integers. The reciprocal lattice is also a Bravais lattice. The vectors
are integers. The reciprocal lattice is also a Bravais lattice. The vectors 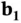 ,
, 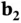 , and
, and 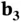 spanning the reciprocal lattice can be constructed explicitly from the lattice vectors 1
spanning the reciprocal lattice can be constructed explicitly from the lattice vectors 1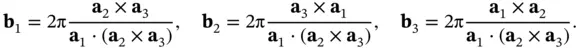
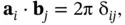
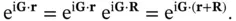
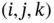 define a plane that is perpendicular to the reciprocal lattice vector
define a plane that is perpendicular to the reciprocal lattice vector 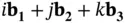 (see Problem 9).
(see Problem 9).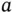 ( Fig. 1.11). We are interested in a function with the periodicity of the lattice, such as the electron concentration
( Fig. 1.11). We are interested in a function with the periodicity of the lattice, such as the electron concentration 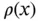 along the chain,
along the chain, 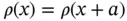 . We can write this as a Fourier series of the form
. We can write this as a Fourier series of the form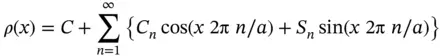
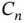 and
and 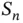 . The sum starts at
. The sum starts at 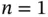 , the constant
, the constant 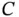 is therefore outside the summation. Using complex coefficients
is therefore outside the summation. Using complex coefficients 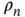 , we can also write this in the more compact form
, we can also write this in the more compact form










