1 ...7 8 9 11 12 13 ...22 It is highly beneficial to use the complex notation for describing the electromagnetic X‐ray waves. For the electric field, a general plane wave can be written as
(1.4) 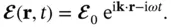
The wave vector 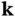 points in the direction of the wave propagation with a length of
points in the direction of the wave propagation with a length of 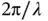 , where
, where 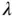 is the wavelength. The convention is that the physical electric field is obtained as the real part of the complex field and the intensity of the wave is obtained as
is the wavelength. The convention is that the physical electric field is obtained as the real part of the complex field and the intensity of the wave is obtained as
(1.5) 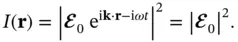
Consider now the situation depicted in Figure 1.10. The source of the X‐rays is far away from the sample at the position 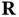 so that the X‐ray wave at the sample can be described as a plane wave. The electric field at a point
so that the X‐ray wave at the sample can be described as a plane wave. The electric field at a point 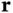 in the crystal at time
in the crystal at time 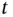 can be written as
can be written as
(1.6) 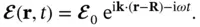
Before we proceed, we can drop the absolute amplitude 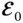 from this expression because we are only interested in relative phase changes. The field at point
from this expression because we are only interested in relative phase changes. The field at point 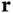 is then
is then
(1.7) 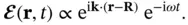
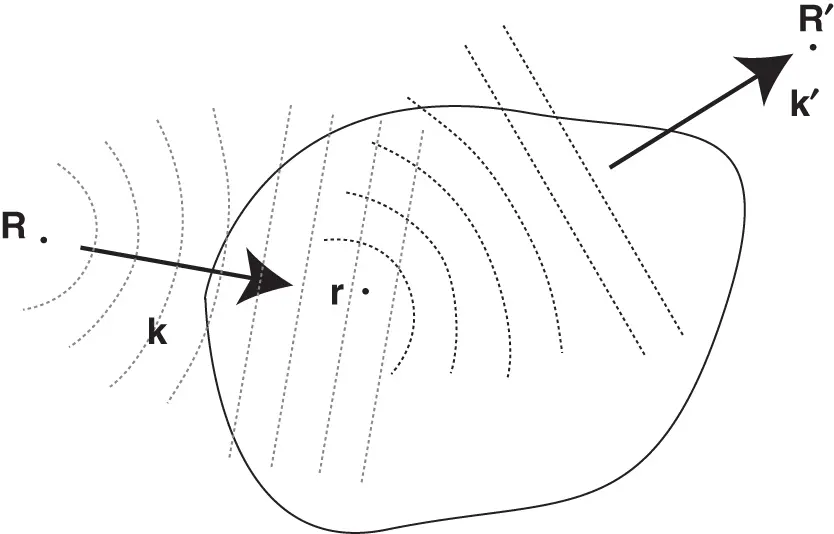
Figure 1.10 Illustration of X‐ray scattering from a sample. The source and detector for the X‐rays are placed at 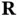 and
and 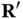 , respectively. Both are very far away from the sample.
, respectively. Both are very far away from the sample.
A small volume element 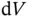 located at
located at 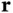 will give rise to scattered waves in all directions. The direction we are interested in is that towards the detector, which we assume to be placed at position
will give rise to scattered waves in all directions. The direction we are interested in is that towards the detector, which we assume to be placed at position 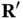 , in the direction of a second wave vector
, in the direction of a second wave vector 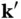 . We assume that the amplitude of the wave scattered in this direction will be proportional to the incoming field from Eq. (1.7)and to a factor
. We assume that the amplitude of the wave scattered in this direction will be proportional to the incoming field from Eq. (1.7)and to a factor 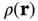 describing the scattering probability and scattering phase. We already know that the scattering of X‐rays proceeds via the electrons in the material, and for our purpose, we can view
describing the scattering probability and scattering phase. We already know that the scattering of X‐rays proceeds via the electrons in the material, and for our purpose, we can view  as the electron concentration in the solid. For the field at the detector, we obtain
as the electron concentration in the solid. For the field at the detector, we obtain
(1.8) 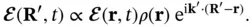
Again, we have assumed that the detector is very far away from the sample so that the scattered wave at the detector can be written as a plane wave. Inserting Eq. (1.7)gives the field at the detector as
(1.9) 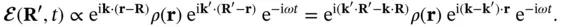
We drop the first factor that does not contain 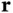 and will thus not play a role for the interference of X‐rays emitted from different positions in the sample. The total wave field at the detector can finally be calculated by integrating over the entire volume
and will thus not play a role for the interference of X‐rays emitted from different positions in the sample. The total wave field at the detector can finally be calculated by integrating over the entire volume 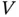 of the crystal. As the detector is far away from the sample, the wave vector
of the crystal. As the detector is far away from the sample, the wave vector 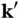 is essentially the same for all points in the sample. The result is therefore
is essentially the same for all points in the sample. The result is therefore
(1.10) 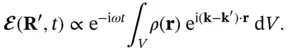
In most cases, it will only be possible to measure the intensity of the X‐rays and not the field amplitude. This intensity is given by
(1.11) 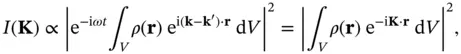
where we have introduced the so‐called scattering vector 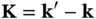 , which is just the difference of the outgoing and incoming wave vectors. Note that although the direction of the wave vector
, which is just the difference of the outgoing and incoming wave vectors. Note that although the direction of the wave vector 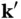 for the scattered waves is different from that of the incoming wave
for the scattered waves is different from that of the incoming wave 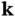 , their lengths are the same because we consider elastic scattering only.
, their lengths are the same because we consider elastic scattering only.
Читать дальше

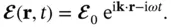
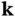 points in the direction of the wave propagation with a length of
points in the direction of the wave propagation with a length of 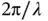 , where
, where 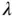 is the wavelength. The convention is that the physical electric field is obtained as the real part of the complex field and the intensity of the wave is obtained as
is the wavelength. The convention is that the physical electric field is obtained as the real part of the complex field and the intensity of the wave is obtained as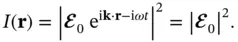
 so that the X‐ray wave at the sample can be described as a plane wave. The electric field at a point
so that the X‐ray wave at the sample can be described as a plane wave. The electric field at a point 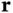 in the crystal at time
in the crystal at time 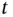 can be written as
can be written as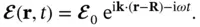
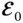 from this expression because we are only interested in relative phase changes. The field at point
from this expression because we are only interested in relative phase changes. The field at point 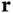 is then
is then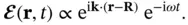

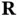 and
and 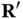 , respectively. Both are very far away from the sample.
, respectively. Both are very far away from the sample.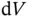 located at
located at 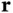 will give rise to scattered waves in all directions. The direction we are interested in is that towards the detector, which we assume to be placed at position
will give rise to scattered waves in all directions. The direction we are interested in is that towards the detector, which we assume to be placed at position 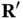 , in the direction of a second wave vector
, in the direction of a second wave vector 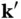 . We assume that the amplitude of the wave scattered in this direction will be proportional to the incoming field from Eq. (1.7)and to a factor
. We assume that the amplitude of the wave scattered in this direction will be proportional to the incoming field from Eq. (1.7)and to a factor 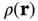 describing the scattering probability and scattering phase. We already know that the scattering of X‐rays proceeds via the electrons in the material, and for our purpose, we can view
describing the scattering probability and scattering phase. We already know that the scattering of X‐rays proceeds via the electrons in the material, and for our purpose, we can view  as the electron concentration in the solid. For the field at the detector, we obtain
as the electron concentration in the solid. For the field at the detector, we obtain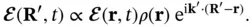
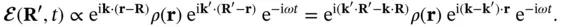
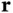 and will thus not play a role for the interference of X‐rays emitted from different positions in the sample. The total wave field at the detector can finally be calculated by integrating over the entire volume
and will thus not play a role for the interference of X‐rays emitted from different positions in the sample. The total wave field at the detector can finally be calculated by integrating over the entire volume 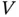 of the crystal. As the detector is far away from the sample, the wave vector
of the crystal. As the detector is far away from the sample, the wave vector 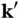 is essentially the same for all points in the sample. The result is therefore
is essentially the same for all points in the sample. The result is therefore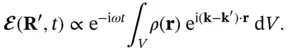
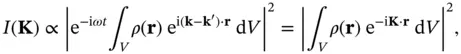
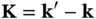 , which is just the difference of the outgoing and incoming wave vectors. Note that although the direction of the wave vector
, which is just the difference of the outgoing and incoming wave vectors. Note that although the direction of the wave vector 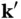 for the scattered waves is different from that of the incoming wave
for the scattered waves is different from that of the incoming wave 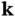 , their lengths are the same because we consider elastic scattering only.
, their lengths are the same because we consider elastic scattering only.










