In the following, we will describe in more detail how this can be achieved. We start with Eq. (1.11), the expression for the diffracted intensity that we had obtained before introducing the reciprocal lattice. But now we know that constructive interference is only observed in an arrangement that corresponds to meeting the Laue condition and we can therefore write the intensity for a particular diffraction spot as
(1.26) 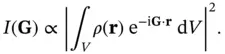
We also know that the crystal consists of many identical unit cells at the positions 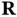 of the Bravais lattice. Therefore, we can split the integral and write it as a sum of integrals over the individual unit cells,
of the Bravais lattice. Therefore, we can split the integral and write it as a sum of integrals over the individual unit cells,
(1.27) 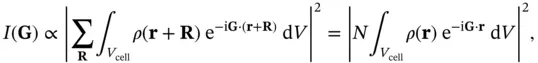
where 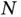 is the number of unit cells in the crystal and we have used the lattice periodicity of
is the number of unit cells in the crystal and we have used the lattice periodicity of 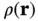 and Eq. (1.14)in the last step. We now assume that the electron density
and Eq. (1.14)in the last step. We now assume that the electron density 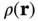 in the unit cell is given by the sum of atomic electron densities
in the unit cell is given by the sum of atomic electron densities 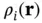 that can be calculated from the atomic wave functions. In doing so, we neglect the fact that some of the electrons form bonds between the atoms and are no longer part of the spherical electron cloud around the atom. If the atoms are not too light, however, the number of these valence electrons is small compared to the total number of electrons and the approximation is appropriate. We can then write
that can be calculated from the atomic wave functions. In doing so, we neglect the fact that some of the electrons form bonds between the atoms and are no longer part of the spherical electron cloud around the atom. If the atoms are not too light, however, the number of these valence electrons is small compared to the total number of electrons and the approximation is appropriate. We can then write
(1.28) 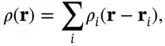
where we sum over the different atoms in the unit cell (i.e. the basis) at positions 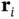 . This permits us to rewrite the integral in Eq. (1.27)as a sum of integrals over the individual atoms in the unit cell
. This permits us to rewrite the integral in Eq. (1.27)as a sum of integrals over the individual atoms in the unit cell
(1.29) 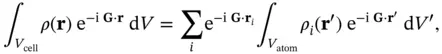
where 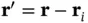 . The two exponential functions give rise to two types of interference. The first describes the interference between the X‐rays scattered by the different atoms in the unit cell, and the second the interference between the X‐rays scattered by the electrons within one atom. The last integral is called the atomic form factorand can be calculated from the atomic properties alone. We therefore see how the diffracted intensity for an assumed structure can be calculated from the atomic form factors and the arrangement of the atoms.
. The two exponential functions give rise to two types of interference. The first describes the interference between the X‐rays scattered by the different atoms in the unit cell, and the second the interference between the X‐rays scattered by the electrons within one atom. The last integral is called the atomic form factorand can be calculated from the atomic properties alone. We therefore see how the diffracted intensity for an assumed structure can be calculated from the atomic form factors and the arrangement of the atoms.
1.3.1.7 The Ewald Construction
In 1913, P. Ewald published an intuitive geometrical construction to visualize the Laue condition [ Eq. (1.25)] and to determine the directions 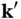 for which constructive interference is to be expected. The construction is shown in Figure 1.12, which represents a cut through the reciprocal lattice; the black points are the reciprocal lattice points. The construction works as follows:
for which constructive interference is to be expected. The construction is shown in Figure 1.12, which represents a cut through the reciprocal lattice; the black points are the reciprocal lattice points. The construction works as follows:
1 We draw the wave vector of the incoming X‐rays such that it ends in the origin of the reciprocal lattice (we may of course choose the point of origin freely).
2 We construct a circle of radius around the starting point of .
3 Wherever the circle touches a reciprocal lattice point, the Laue condition is fulfilled.
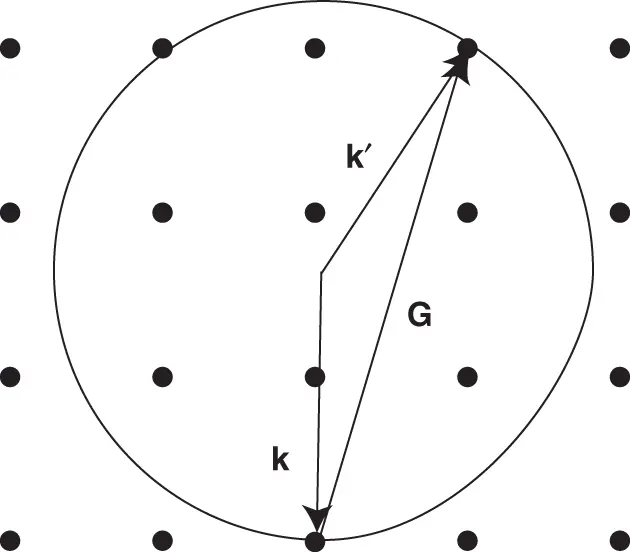
Figure 1.12 Ewald construction for finding the directions in which constructive interference can be observed. The dots represent the reciprocal lattice. The arrows labeled 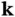 and
and 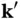 are the wave vectors of the incoming and scattered X‐rays, respectively.
are the wave vectors of the incoming and scattered X‐rays, respectively.
For a three‐dimensional crystal, this construction has to be carried out in different planes, of course. The figure clearly shows that Eq. (1.25)is a very stringent condition: It is not likely for the sphere to hit a second reciprocal lattice point, which means that constructive interference is expected for very few directions. As in the Bragg description, we see that the wavelength of the X‐rays has to be sufficiently small ( 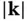 has to be sufficiently large) for any constructive interference to occur.
has to be sufficiently large) for any constructive interference to occur.
Practical X‐ray diffraction experiments are often carried out in such a way that many constructive interference maxima are observed despite the strong restrictions imposed by the Laue condition, Eq. (1.25). For example, this can be achieved by using a wide range of X‐ray wavelengths, i.e. non‐monochromatic radiation, or by performing a diffraction experiment not on a single crystal but on a powder of randomly oriented small crystals.
1.3.1.8 Relation Between Bragg and Laue Theory
We conclude our treatment of X‐ray diffraction by showing that the Bragg description of X‐ray diffraction is just a special case of the Laue description. We start by noting that the Laue condition in Eq. (1.25)consists, in fact, of three separate conditions for the three components of the vectors. In the Bragg experiment, two of these conditions are automatically fulfilled because of the specular geometry: The wave vector change parallel to the lattice planes is zero. So, the vector Equation 1.25reduces to the scalar equation
(1.30) 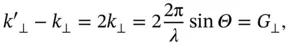
where 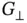 is a reciprocal lattice vector perpendicular to the lattice planes. We have seen in Section 1.3.1.4that such a reciprocal lattice vector exists for any set of planes. The planes can be defined by their Miller indices
is a reciprocal lattice vector perpendicular to the lattice planes. We have seen in Section 1.3.1.4that such a reciprocal lattice vector exists for any set of planes. The planes can be defined by their Miller indices 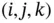 or by the reciprocal lattice vector
or by the reciprocal lattice vector 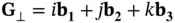 that is perpendicular to the planes (see Problem 9). The shortest possible
that is perpendicular to the planes (see Problem 9). The shortest possible 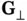 has a length of
has a length of 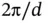 with
with 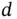 being the distance between the planes, but any integer multiple of this will also work. Thus, if we insert
being the distance between the planes, but any integer multiple of this will also work. Thus, if we insert 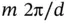 for
for 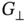 into Eq. (1.30), we obtain the usual form of the Bragg condition in Eq. (1.3).
into Eq. (1.30), we obtain the usual form of the Bragg condition in Eq. (1.3).
Читать дальше

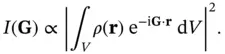
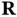 of the Bravais lattice. Therefore, we can split the integral and write it as a sum of integrals over the individual unit cells,
of the Bravais lattice. Therefore, we can split the integral and write it as a sum of integrals over the individual unit cells,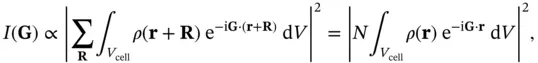
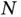 is the number of unit cells in the crystal and we have used the lattice periodicity of
is the number of unit cells in the crystal and we have used the lattice periodicity of 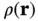 and Eq. (1.14)in the last step. We now assume that the electron density
and Eq. (1.14)in the last step. We now assume that the electron density 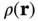 in the unit cell is given by the sum of atomic electron densities
in the unit cell is given by the sum of atomic electron densities 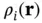 that can be calculated from the atomic wave functions. In doing so, we neglect the fact that some of the electrons form bonds between the atoms and are no longer part of the spherical electron cloud around the atom. If the atoms are not too light, however, the number of these valence electrons is small compared to the total number of electrons and the approximation is appropriate. We can then write
that can be calculated from the atomic wave functions. In doing so, we neglect the fact that some of the electrons form bonds between the atoms and are no longer part of the spherical electron cloud around the atom. If the atoms are not too light, however, the number of these valence electrons is small compared to the total number of electrons and the approximation is appropriate. We can then write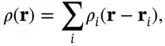
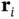 . This permits us to rewrite the integral in Eq. (1.27)as a sum of integrals over the individual atoms in the unit cell
. This permits us to rewrite the integral in Eq. (1.27)as a sum of integrals over the individual atoms in the unit cell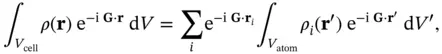
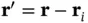 . The two exponential functions give rise to two types of interference. The first describes the interference between the X‐rays scattered by the different atoms in the unit cell, and the second the interference between the X‐rays scattered by the electrons within one atom. The last integral is called the atomic form factorand can be calculated from the atomic properties alone. We therefore see how the diffracted intensity for an assumed structure can be calculated from the atomic form factors and the arrangement of the atoms.
. The two exponential functions give rise to two types of interference. The first describes the interference between the X‐rays scattered by the different atoms in the unit cell, and the second the interference between the X‐rays scattered by the electrons within one atom. The last integral is called the atomic form factorand can be calculated from the atomic properties alone. We therefore see how the diffracted intensity for an assumed structure can be calculated from the atomic form factors and the arrangement of the atoms.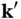 for which constructive interference is to be expected. The construction is shown in Figure 1.12, which represents a cut through the reciprocal lattice; the black points are the reciprocal lattice points. The construction works as follows:
for which constructive interference is to be expected. The construction is shown in Figure 1.12, which represents a cut through the reciprocal lattice; the black points are the reciprocal lattice points. The construction works as follows:
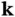 and
and 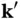 are the wave vectors of the incoming and scattered X‐rays, respectively.
are the wave vectors of the incoming and scattered X‐rays, respectively.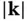 has to be sufficiently large) for any constructive interference to occur.
has to be sufficiently large) for any constructive interference to occur.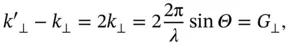
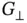 is a reciprocal lattice vector perpendicular to the lattice planes. We have seen in Section 1.3.1.4that such a reciprocal lattice vector exists for any set of planes. The planes can be defined by their Miller indices
is a reciprocal lattice vector perpendicular to the lattice planes. We have seen in Section 1.3.1.4that such a reciprocal lattice vector exists for any set of planes. The planes can be defined by their Miller indices 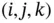 or by the reciprocal lattice vector
or by the reciprocal lattice vector 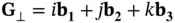 that is perpendicular to the planes (see Problem 9). The shortest possible
that is perpendicular to the planes (see Problem 9). The shortest possible 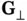 has a length of
has a length of 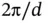 with
with 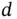 being the distance between the planes, but any integer multiple of this will also work. Thus, if we insert
being the distance between the planes, but any integer multiple of this will also work. Thus, if we insert 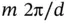 for
for 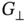 into Eq. (1.30), we obtain the usual form of the Bragg condition in Eq. (1.3).
into Eq. (1.30), we obtain the usual form of the Bragg condition in Eq. (1.3).










