6 1.6 The reciprocal lattice: Using the explicit definition of the reciprocal lattice in Eq. (1.16), show first that Eq. (1.17)is obeyed and then proceed, using this relation, to show that the reciprocal lattice defined by Eq. (1.16)does indeed meet the condition from Eq. (1.13).
7 1.7 The reciprocal lattice: For a two‐dimensional Bravais lattice(1.31) the reciprocal lattice is also two‐dimensional:(1.32) Often, the most practical way to construct the reciprocal lattice is to use the relation(1.33) which remains valid in the two‐dimensional case. Find the reciprocal lattices for the three cases displayed in Figure 1.17. Figure 1.17 Two‐dimensional Bravais lattices.
8 1.8 Lattice‐periodic functions: Figure 1.11shows two lattice‐periodic functions and the Fourier coefficients generating these functions. The functions have been calculated from the coefficients using Eq. (1.20). (a) Write down the specific Fourier series corresponding to the lower half of Fig. 1.11and make sure that the result is correct by plotting in the same interval as in the figure, from to (you may choose ). (b) Now try the reverse operation by numerically calculating the Fourier transform of the obtained . Display the resulting . You will find that it does not match the right‐hand side of Fig. 1.11: Instead of functions at the reciprocal lattice points, you will obtain quite broad peaks. Why is this so? What would be needed to narrow these peaks? Demonstrate how this can be achieved. (c)* Discuss the implications for the observed intensity in X‐ray diffraction. To this end, note that upon fulfilling the Laue condition, the diffracted intensity around a reciprocal lattice vector as in Eq. (1.26)corresponds to the squared norm of the scattering density's Fourier transformation.
9 1.9 Miller indices: We have stated that the reciprocal lattice vector is perpendicular to the lattice plane given by the Miller indices . (a) Verify that this is correct for the lattice planes drawn in Figure 1.9. (b)* Show that this statement is universally valid.
1 1The denominator is chosen to be the same for all three reciprocal lattice vectors, but note that the combination of dot product and cross product is “circular” such that .
2 2denotes Kronecker's delta, which is 1 for and zero otherwise.
After studying the structures of crystals, we now discuss the different mechanisms that lead to bonding between atoms such that they form these structures. We will encounter different scenarios such as ionic, covalent, or metallic bonding. It has to be kept in mind, however, that these are only idealized limiting cases. More often than not, mixed bonding types are encountered – for example, a combination of metallic and covalent bonding in the transition metals.
As in conventional chemistry, only a fraction of the electrons, the so‐called valence electrons,participate in the bonding. These are the electrons in the outermost shell(s) of an atom. The electrons in the inner shells, or core electrons,are bound so tightly to the nucleus that their energies and wave functions are hardly influenced by the presence of other atoms in their neighborhood.
2.1 Attractive and Repulsive Forces
Two different forces must be present to establish bonding in a solid or in a molecule. An attractive force is necessary for any bonding. Different types of attractive forces will be discussed in the following sections. A repulsive force, on the other hand, is required in order to keep the atoms from getting too close to each other. A simple expression for an interatomic potentialcan thus be written as
(2.1) 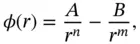
where 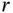 is the distance between the atoms and
is the distance between the atoms and 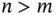 – that is, the repulsive part has to prevail for short distances (sometimes, this is achieved by assuming an exponential repulsion potential). Such a potential and the resulting force are shown in Figure 2.1. The reason for the strong repulsion at short distances is the Pauli exclusion principle. For a strong overlap of the electron clouds of two atoms, which will occur at short distances, the wave functions have to change in order to become orthogonal to each other, because the Pauli principle does not allow more than two electrons to exist in the same (spatial) quantum state. This orthogonalization requires much energy, hence the strong repulsion.
– that is, the repulsive part has to prevail for short distances (sometimes, this is achieved by assuming an exponential repulsion potential). Such a potential and the resulting force are shown in Figure 2.1. The reason for the strong repulsion at short distances is the Pauli exclusion principle. For a strong overlap of the electron clouds of two atoms, which will occur at short distances, the wave functions have to change in order to become orthogonal to each other, because the Pauli principle does not allow more than two electrons to exist in the same (spatial) quantum state. This orthogonalization requires much energy, hence the strong repulsion.
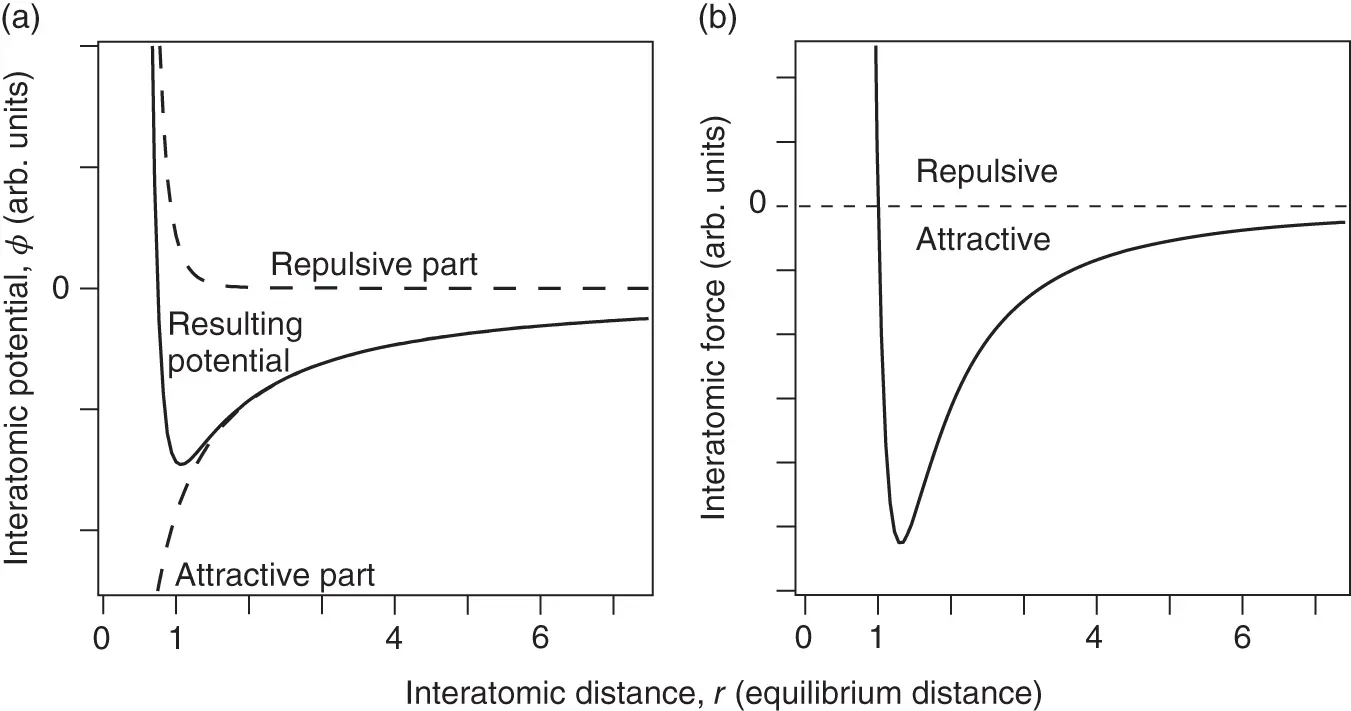
Figure 2.1 (a) Typical interatomic potential 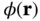 for bonding in solids according to Eq. (2.1) with
for bonding in solids according to Eq. (2.1) with 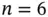 and
and 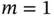 . (b) Resulting force, that is,
. (b) Resulting force, that is, 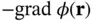 .
.
Ionic bonding involves the transfer of electrons from an electropositive atom to an electronegative atom. The bonding force is the Coulomb attraction between the two resulting ions. Turning the atoms into ions usually costs some energy. In the case of NaCl, the ionization energy of Na is 5.1 eV and the electron affinity of Cl is 3.6 eV. The net energy cost for creating a pair of ions is thus 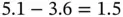 eV. The energy gain is given by the Coulomb interaction between the resulting ions. For just one Na and one Cl ion separated by the distance found in the actual crystal structure of NaCl (
eV. The energy gain is given by the Coulomb interaction between the resulting ions. For just one Na and one Cl ion separated by the distance found in the actual crystal structure of NaCl ( 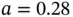 nm), this is
nm), this is 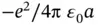 , which amounts to 5.1 eV.
, which amounts to 5.1 eV.
Knowing the crystal structure for NaCl, we can also calculate the electrostatic energy gain for forming an entire crystal. Consider one Na ion at the center of the NaCl cube in Figure 1.5. It is surrounded by six Cl ions at a distance of 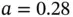 nm, leading to an electrostatic energy gain of
nm, leading to an electrostatic energy gain of 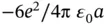 . At a distance of
. At a distance of 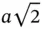 , there are 12 other Na ions, giving rise to an energy increase of
, there are 12 other Na ions, giving rise to an energy increase of 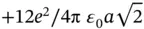 . Next, one finds eight Cl ions that again decrease the energy. Eventually, this series converges and the total energy gain is
. Next, one finds eight Cl ions that again decrease the energy. Eventually, this series converges and the total energy gain is
Читать дальше

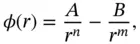
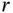 is the distance between the atoms and
is the distance between the atoms and 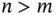 – that is, the repulsive part has to prevail for short distances (sometimes, this is achieved by assuming an exponential repulsion potential). Such a potential and the resulting force are shown in Figure 2.1. The reason for the strong repulsion at short distances is the Pauli exclusion principle. For a strong overlap of the electron clouds of two atoms, which will occur at short distances, the wave functions have to change in order to become orthogonal to each other, because the Pauli principle does not allow more than two electrons to exist in the same (spatial) quantum state. This orthogonalization requires much energy, hence the strong repulsion.
– that is, the repulsive part has to prevail for short distances (sometimes, this is achieved by assuming an exponential repulsion potential). Such a potential and the resulting force are shown in Figure 2.1. The reason for the strong repulsion at short distances is the Pauli exclusion principle. For a strong overlap of the electron clouds of two atoms, which will occur at short distances, the wave functions have to change in order to become orthogonal to each other, because the Pauli principle does not allow more than two electrons to exist in the same (spatial) quantum state. This orthogonalization requires much energy, hence the strong repulsion.
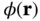 for bonding in solids according to Eq. (2.1) with
for bonding in solids according to Eq. (2.1) with 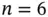 and
and 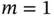 . (b) Resulting force, that is,
. (b) Resulting force, that is, 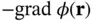 .
.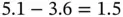 eV. The energy gain is given by the Coulomb interaction between the resulting ions. For just one Na and one Cl ion separated by the distance found in the actual crystal structure of NaCl (
eV. The energy gain is given by the Coulomb interaction between the resulting ions. For just one Na and one Cl ion separated by the distance found in the actual crystal structure of NaCl ( 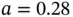 nm), this is
nm), this is 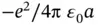 , which amounts to 5.1 eV.
, which amounts to 5.1 eV.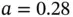 nm, leading to an electrostatic energy gain of
nm, leading to an electrostatic energy gain of 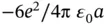 . At a distance of
. At a distance of 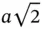 , there are 12 other Na ions, giving rise to an energy increase of
, there are 12 other Na ions, giving rise to an energy increase of 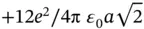 . Next, one finds eight Cl ions that again decrease the energy. Eventually, this series converges and the total energy gain is
. Next, one finds eight Cl ions that again decrease the energy. Eventually, this series converges and the total energy gain is










