(2.4) 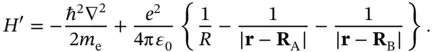
This Hamiltonian is that of an electron moving in the Coulomb potential of two protons separated by a distance 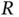 . The electrostatic repulsion of the nuclei (the
. The electrostatic repulsion of the nuclei (the 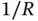 term) does not depend on the position of the electron and just leads to an energy offset that could be treated separately. We choose to leave it in the Hamiltonian, though, as we want to inspect the dependence of the resulting energy levels on
term) does not depend on the position of the electron and just leads to an energy offset that could be treated separately. We choose to leave it in the Hamiltonian, though, as we want to inspect the dependence of the resulting energy levels on 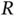 later.
later.
We can calculate an approximate ground‐state solution to the Schrödinger equation 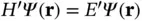 by writing
by writing 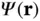 as a linear combination of the atomic 1s wave functions of the two atoms,
as a linear combination of the atomic 1s wave functions of the two atoms, 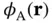 and
and 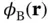 . This approach is commonly known as linear combination of atomic orbitals (LCAO).Our ansatz is thus
. This approach is commonly known as linear combination of atomic orbitals (LCAO).Our ansatz is thus
(2.5) 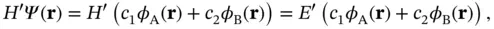
where 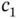 and
and 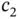 are constants. Multiplying this equation from the left with either
are constants. Multiplying this equation from the left with either 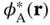 or
or 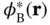 and integrating gives two algebraic equations
and integrating gives two algebraic equations
(2.6) 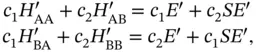
where we have introduced the so‐called overlap integral 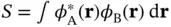 , as well as the abbreviations
, as well as the abbreviations 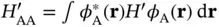 and correspondingly for
and correspondingly for 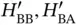 and
and 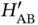 . As the two nuclei at
. As the two nuclei at  and
and 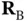 are completely equivalent, we can simplify this by noticing that
are completely equivalent, we can simplify this by noticing that 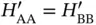 and
and 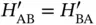 . With this, Eq. (2.6) becomes
. With this, Eq. (2.6) becomes
(2.7) 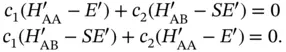
This equation system has a nontrivial solution when the determinant of the coefficient matrix vanishes. This gives two possible solutions
(2.8) 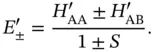
With these solutions, we can calculate the relation between the coefficients 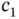 and
and 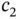 from Eq. (2.7), and we find that
from Eq. (2.7), and we find that 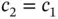 for the “
for the “ 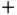 ” solution and
” solution and 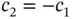 for the “
for the “  ” solution (see Problem 3 and note that
” solution (see Problem 3 and note that 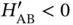 ).
).
The energy levels and wave functions from this calculation are illustrated in Figure 2.2a. For a large distance 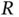 between the nuclei, the overlap integral
between the nuclei, the overlap integral 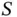 and the matrix element
and the matrix element 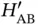 vanish and the only solution is
vanish and the only solution is 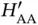 . This makes sense as the second proton is far away from
. This makes sense as the second proton is far away from 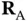 , so
, so 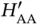 is approximately the ground state energy of atomic hydrogen. A corresponding solution does, of course, exist for the electron located on the other proton. For a short distance
is approximately the ground state energy of atomic hydrogen. A corresponding solution does, of course, exist for the electron located on the other proton. For a short distance 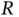 , on the other hand, this energy level splits up into the bonding and antibonding molecular states
, on the other hand, this energy level splits up into the bonding and antibonding molecular states 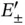 . The single electron will occupy the lower level
. The single electron will occupy the lower level 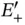 and this will result in the energy gain of covalent bonding. The wave function corresponding to this is the one for which
and this will result in the energy gain of covalent bonding. The wave function corresponding to this is the one for which 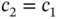 , which increases the electron density between the nuclei. The wave function corresponding to the antibonding upper energy level is constructed by choosing
, which increases the electron density between the nuclei. The wave function corresponding to the antibonding upper energy level is constructed by choosing 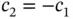 , and it shows the characteristics of an antibonding state with a node between the two nuclei.
, and it shows the characteristics of an antibonding state with a node between the two nuclei.
Читать дальше

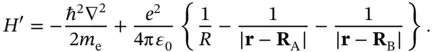
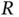 . The electrostatic repulsion of the nuclei (the
. The electrostatic repulsion of the nuclei (the 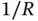 term) does not depend on the position of the electron and just leads to an energy offset that could be treated separately. We choose to leave it in the Hamiltonian, though, as we want to inspect the dependence of the resulting energy levels on
term) does not depend on the position of the electron and just leads to an energy offset that could be treated separately. We choose to leave it in the Hamiltonian, though, as we want to inspect the dependence of the resulting energy levels on 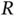 later.
later.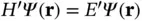 by writing
by writing 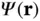 as a linear combination of the atomic 1s wave functions of the two atoms,
as a linear combination of the atomic 1s wave functions of the two atoms, 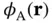 and
and 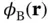 . This approach is commonly known as linear combination of atomic orbitals (LCAO).Our ansatz is thus
. This approach is commonly known as linear combination of atomic orbitals (LCAO).Our ansatz is thus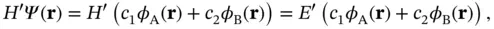
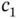 and
and 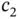 are constants. Multiplying this equation from the left with either
are constants. Multiplying this equation from the left with either 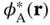 or
or 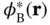 and integrating gives two algebraic equations
and integrating gives two algebraic equations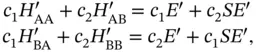
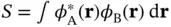 , as well as the abbreviations
, as well as the abbreviations 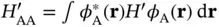 and correspondingly for
and correspondingly for 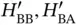 and
and 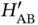 . As the two nuclei at
. As the two nuclei at  and
and 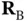 are completely equivalent, we can simplify this by noticing that
are completely equivalent, we can simplify this by noticing that 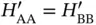 and
and 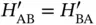 . With this, Eq. (2.6) becomes
. With this, Eq. (2.6) becomes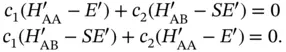
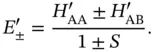
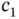 and
and 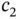 from Eq. (2.7), and we find that
from Eq. (2.7), and we find that 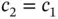 for the “
for the “ 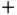 ” solution and
” solution and 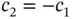 for the “
for the “  ” solution (see Problem 3 and note that
” solution (see Problem 3 and note that 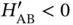 ).
).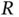 between the nuclei, the overlap integral
between the nuclei, the overlap integral 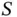 and the matrix element
and the matrix element 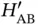 vanish and the only solution is
vanish and the only solution is 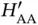 . This makes sense as the second proton is far away from
. This makes sense as the second proton is far away from 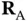 , so
, so 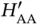 is approximately the ground state energy of atomic hydrogen. A corresponding solution does, of course, exist for the electron located on the other proton. For a short distance
is approximately the ground state energy of atomic hydrogen. A corresponding solution does, of course, exist for the electron located on the other proton. For a short distance 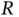 , on the other hand, this energy level splits up into the bonding and antibonding molecular states
, on the other hand, this energy level splits up into the bonding and antibonding molecular states 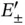 . The single electron will occupy the lower level
. The single electron will occupy the lower level 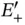 and this will result in the energy gain of covalent bonding. The wave function corresponding to this is the one for which
and this will result in the energy gain of covalent bonding. The wave function corresponding to this is the one for which 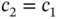 , which increases the electron density between the nuclei. The wave function corresponding to the antibonding upper energy level is constructed by choosing
, which increases the electron density between the nuclei. The wave function corresponding to the antibonding upper energy level is constructed by choosing 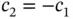 , and it shows the characteristics of an antibonding state with a node between the two nuclei.
, and it shows the characteristics of an antibonding state with a node between the two nuclei.










