The detailed calculation is quite lengthy and shall not be given here. 1 The resulting ground‐state energies for the singlet and triplet states can be written as
(2.12) 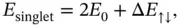
(2.13) 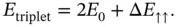
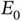 is the ground‐state energy for one hydrogen atom; it is multiplied by two because we start with two atoms. The energies
is the ground‐state energy for one hydrogen atom; it is multiplied by two because we start with two atoms. The energies 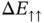 and
and 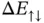 are also shown in Figure 2.4.
are also shown in Figure 2.4. 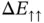 is always larger than zero and does not lead to any chemical bonding.
is always larger than zero and does not lead to any chemical bonding. 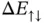 , on the other hand, shows a minimum with negative energy at approximately
, on the other hand, shows a minimum with negative energy at approximately 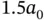 . This is the bonding state.
. This is the bonding state.
For long distances between the nuclei, Eqs. (2.12) and ( 2.13) can be rewritten in the form
(2.14) 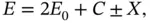
where the 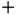 and
and  signs apply to the singlet and triplet state, respectively. In this representation, the energy change upon bonding contains two contributions, of which one depends on the relative spin orientations of the electrons (
signs apply to the singlet and triplet state, respectively. In this representation, the energy change upon bonding contains two contributions, of which one depends on the relative spin orientations of the electrons ( 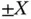 ) and the other does not (
) and the other does not ( 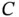 ). The energy difference between the two states is then given by
). The energy difference between the two states is then given by 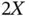 , where
, where 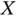 is called the exchange energy.In the case of the hydrogen molecule, the exchange energy is always negative. Equation ( 2.14) is a remarkable result, because it means that the energy of the system depends on the relative orientation of the spins, even though these spins are not explicitly mentioned in the Schrödinger equation.
is called the exchange energy.In the case of the hydrogen molecule, the exchange energy is always negative. Equation ( 2.14) is a remarkable result, because it means that the energy of the system depends on the relative orientation of the spins, even though these spins are not explicitly mentioned in the Schrödinger equation.
We will encounter similar concepts in the chapter about magnetism, where the underlying principle for magnetic ordering is very similar to what we see here: Through the exchange energy, the total energy of a system of electrons depends on their relative spin orientations, and therefore a particular ordered spin configuration is energetically favored. For two electrons, the “magnetic” character is purely given by the sign of 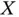 . For negative
. For negative 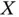 , the coupling with two opposite spins is favorable (the “antiferromagnetic” case), whereas a positive
, the coupling with two opposite spins is favorable (the “antiferromagnetic” case), whereas a positive 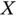 would lead to a situation where two parallel spins give the lowest energy (the “ferromagnetic” case).
would lead to a situation where two parallel spins give the lowest energy (the “ferromagnetic” case).
Finally, it is interesting to compare the single‐electron solution for the  ion to the two‐electron Heitler‐London solution for
ion to the two‐electron Heitler‐London solution for  . The curves for the bonding energy levels in Figures 2.2and 2.4are strikingly similar, especially if we expect a second electron in the
. The curves for the bonding energy levels in Figures 2.2and 2.4are strikingly similar, especially if we expect a second electron in the 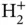 ion to show approximately the same energy gain as the first one (and hence a minimum of the total energy that is twice as deep). The similarity suggests that the interaction between the two electrons is not too important. Qualitatively, we can understand this in the following way: For
ion to show approximately the same energy gain as the first one (and hence a minimum of the total energy that is twice as deep). The similarity suggests that the interaction between the two electrons is not too important. Qualitatively, we can understand this in the following way: For 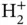 , there is no second electron and for the singlet state of
, there is no second electron and for the singlet state of  , the symmetry of the wave function ensures that the two electrons are never at the same place, reducing their interaction. A noticeable difference between
, the symmetry of the wave function ensures that the two electrons are never at the same place, reducing their interaction. A noticeable difference between 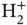 and
and 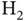 is the position of the energy minimum, i.e. the equilibrium distance between the nuclei, which is significantly smaller in the case of
is the position of the energy minimum, i.e. the equilibrium distance between the nuclei, which is significantly smaller in the case of 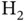 . This does not come as a surprise. After all, two electrons contribute to the attraction. Despite the similarity between the curves, one needs to keep in mind that they represent two entirely different things: Figure 2.2shows the energy levels of one single electron and we are not allowed to multiply the curves by a factor of two to obtain the energy for two electrons (even though we just contemplated this). The curves in Figure 2.4represent the energy levels for two electrons. We cannot split this into contributions for the separate energies of two single electrons.
. This does not come as a surprise. After all, two electrons contribute to the attraction. Despite the similarity between the curves, one needs to keep in mind that they represent two entirely different things: Figure 2.2shows the energy levels of one single electron and we are not allowed to multiply the curves by a factor of two to obtain the energy for two electrons (even though we just contemplated this). The curves in Figure 2.4represent the energy levels for two electrons. We cannot split this into contributions for the separate energies of two single electrons.
In metals, the valence electrons of the atoms are removed from the ion cores, but in contrast to ionic solids, there are no electronegative ions to bind them. Therefore, they are free to migrate between the ionic cores. These delocalized valence electrons are involved in the conduction of electricity and are therefore often called conduction electrons.One can expect metals to form from elements for which the energy necessary to remove outer electrons is not too big. Nevertheless, this removal always costs some energy that has to be more than compensated by the resulting bonding. Explaining the energy gain from the bonding in an intuitive manner is difficult, but we will at least try to make it plausible. Obviously, the ultimate reason must be some sort of energy lowering.
One energy contribution that is lowered is the kinetic energy of the conduction electrons. Consider the kinetic energy contribution in a Hamiltonian, 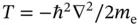 . A matrix element
. A matrix element 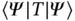 measures the kinetic energy of a particle, and
measures the kinetic energy of a particle, and 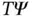 is proportional to the second spatial derivative of the wave function, that is, its curvature. For an electron localized at an atom, the curvature of the wave function is much larger than for a nearly free electron in a metal, and this is the origin of the energy gain. A simple implementation of this idea is found in Problem 4, which inspects the lowering of the kinetic energy resulting from delocalization of an electron over the size of a typical crystal unit cell rather than just over the volume of an atom.
is proportional to the second spatial derivative of the wave function, that is, its curvature. For an electron localized at an atom, the curvature of the wave function is much larger than for a nearly free electron in a metal, and this is the origin of the energy gain. A simple implementation of this idea is found in Problem 4, which inspects the lowering of the kinetic energy resulting from delocalization of an electron over the size of a typical crystal unit cell rather than just over the volume of an atom.
Читать дальше

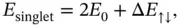
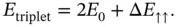
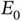 is the ground‐state energy for one hydrogen atom; it is multiplied by two because we start with two atoms. The energies
is the ground‐state energy for one hydrogen atom; it is multiplied by two because we start with two atoms. The energies 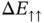 and
and 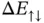 are also shown in Figure 2.4.
are also shown in Figure 2.4. 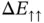 is always larger than zero and does not lead to any chemical bonding.
is always larger than zero and does not lead to any chemical bonding. 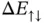 , on the other hand, shows a minimum with negative energy at approximately
, on the other hand, shows a minimum with negative energy at approximately 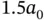 . This is the bonding state.
. This is the bonding state.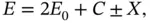
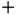 and
and  signs apply to the singlet and triplet state, respectively. In this representation, the energy change upon bonding contains two contributions, of which one depends on the relative spin orientations of the electrons (
signs apply to the singlet and triplet state, respectively. In this representation, the energy change upon bonding contains two contributions, of which one depends on the relative spin orientations of the electrons ( 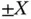 ) and the other does not (
) and the other does not ( 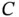 ). The energy difference between the two states is then given by
). The energy difference between the two states is then given by 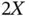 , where
, where 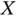 is called the exchange energy.In the case of the hydrogen molecule, the exchange energy is always negative. Equation ( 2.14) is a remarkable result, because it means that the energy of the system depends on the relative orientation of the spins, even though these spins are not explicitly mentioned in the Schrödinger equation.
is called the exchange energy.In the case of the hydrogen molecule, the exchange energy is always negative. Equation ( 2.14) is a remarkable result, because it means that the energy of the system depends on the relative orientation of the spins, even though these spins are not explicitly mentioned in the Schrödinger equation.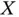 . For negative
. For negative 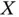 , the coupling with two opposite spins is favorable (the “antiferromagnetic” case), whereas a positive
, the coupling with two opposite spins is favorable (the “antiferromagnetic” case), whereas a positive 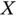 would lead to a situation where two parallel spins give the lowest energy (the “ferromagnetic” case).
would lead to a situation where two parallel spins give the lowest energy (the “ferromagnetic” case). ion to the two‐electron Heitler‐London solution for
ion to the two‐electron Heitler‐London solution for  . The curves for the bonding energy levels in Figures 2.2and 2.4are strikingly similar, especially if we expect a second electron in the
. The curves for the bonding energy levels in Figures 2.2and 2.4are strikingly similar, especially if we expect a second electron in the 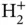 ion to show approximately the same energy gain as the first one (and hence a minimum of the total energy that is twice as deep). The similarity suggests that the interaction between the two electrons is not too important. Qualitatively, we can understand this in the following way: For
ion to show approximately the same energy gain as the first one (and hence a minimum of the total energy that is twice as deep). The similarity suggests that the interaction between the two electrons is not too important. Qualitatively, we can understand this in the following way: For 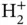 , there is no second electron and for the singlet state of
, there is no second electron and for the singlet state of  , the symmetry of the wave function ensures that the two electrons are never at the same place, reducing their interaction. A noticeable difference between
, the symmetry of the wave function ensures that the two electrons are never at the same place, reducing their interaction. A noticeable difference between 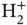 and
and 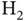 is the position of the energy minimum, i.e. the equilibrium distance between the nuclei, which is significantly smaller in the case of
is the position of the energy minimum, i.e. the equilibrium distance between the nuclei, which is significantly smaller in the case of 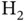 . This does not come as a surprise. After all, two electrons contribute to the attraction. Despite the similarity between the curves, one needs to keep in mind that they represent two entirely different things: Figure 2.2shows the energy levels of one single electron and we are not allowed to multiply the curves by a factor of two to obtain the energy for two electrons (even though we just contemplated this). The curves in Figure 2.4represent the energy levels for two electrons. We cannot split this into contributions for the separate energies of two single electrons.
. This does not come as a surprise. After all, two electrons contribute to the attraction. Despite the similarity between the curves, one needs to keep in mind that they represent two entirely different things: Figure 2.2shows the energy levels of one single electron and we are not allowed to multiply the curves by a factor of two to obtain the energy for two electrons (even though we just contemplated this). The curves in Figure 2.4represent the energy levels for two electrons. We cannot split this into contributions for the separate energies of two single electrons.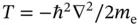 . A matrix element
. A matrix element 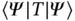 measures the kinetic energy of a particle, and
measures the kinetic energy of a particle, and 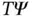 is proportional to the second spatial derivative of the wave function, that is, its curvature. For an electron localized at an atom, the curvature of the wave function is much larger than for a nearly free electron in a metal, and this is the origin of the energy gain. A simple implementation of this idea is found in Problem 4, which inspects the lowering of the kinetic energy resulting from delocalization of an electron over the size of a typical crystal unit cell rather than just over the volume of an atom.
is proportional to the second spatial derivative of the wave function, that is, its curvature. For an electron localized at an atom, the curvature of the wave function is much larger than for a nearly free electron in a metal, and this is the origin of the energy gain. A simple implementation of this idea is found in Problem 4, which inspects the lowering of the kinetic energy resulting from delocalization of an electron over the size of a typical crystal unit cell rather than just over the volume of an atom.










