Philip Hofmann - Solid State Physics

The other contribution to electrons' energy is their potential energy. One might think that the average electrostatic potential experienced by any single electron in a solid is almost zero because there are (almost) as many other electrons as there are ions with the same overall amount of charge. This reasoning turns out to be wrong, however. In fact, the electrons experience an overall attractive potential. The reason is again partly due to the Pauli principle, which – in simple terms – does not permit two electrons with the same spin orientation to occupy the same position [see Eq. (2.10)] and therefore requires the electrons to avoid each other. In addition to this, there is also a direct Coulomb interaction between the electrons, which also makes them sidestep each other. We will discuss this in more detail when dealing with magnetism.

We can now also understand why metals prefer close‐packed structures. First of all, metallic bonding does not have any directional preference. Second, close‐packed structures secure the highest possible overlap between the valence orbitals of the atoms, maximizing the delocalization of the electrons and thereby the kinetic energy gain. The resulting structures also maximize the number of nearest neighbors for any given atom, again giving rise to strongly delocalized states.

The picture of metallic bonding described here holds mainly for simple metalswith only s and p electrons in the outer shells. For these, metallic bonding is not as strong as covalent or ionic bonding, but the cohesive energy can still amount to 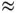1–2 eV per atom. Stronger bonding is found in transition metals,i.e. metals that have partially filled d shells in addition to the s and p electrons (an overview of the cohesive energies is provided in Figure 4.16). The explanation for this is that a mixed bonding situation arises in these cases. The s and p electrons turn into delocalized metallic conduction electrons, whereas the d electrons create more localized, covalent‐type bonds.

Hydrogen atoms possess only one electron and can form only one covalent bond. If this bond is formed with a very electronegative atom (like F or O), the electron is mostly located close to that atom and the hydrogen nucleus represents more or less an isolated positive (partial) charge. This can lead to a considerable charge density because of its small size, and it can therefore attract negative (partial) charges in other molecules to form an electrostatic bond. This type of bonding is called hydrogen bonding. It is usually quite weak, but in some cases, the cohesive energy can be up to several hundred meV per atom. It is responsible for the intermolecular attraction in (liquid and solid) water and for the bonding of the double helix strands in DNA.

The term van der Waals bonding refers to a weak and purely quantum‐mechanical effect. The electron cloud around an atom or a molecule has no static charge distribution but one governed by quantum‐mechanical fluctuations. A simple atom with a closed shell can thus be viewed as a fluctuating dipole. The field of this dipole can polarize other atoms nearby, and the interaction of the two neighboring dipoles reduces the total energy of the pair of dipoles, that is, it can lead to bonding. This type of interaction is present in every solid but is much weaker than ionic, covalent, or metallic bonding. Typical binding energies per atom are in the meV range and, therefore, pure van der Waals bonding is only observable for solids that do not show any other bonding type – for example, noble gases. Van der Waals crystals of noble gases can only exist at very low temperatures. Since they are formed from inert atoms without any “real” bonds, they represent an almost ideal case of close‐packed spheres and they all crystallize in the face‐centered cubic structure. Van der Waals bonding can also be important in layered crystals such as graphite. Here, charge fluctuations may arise in the stacked graphene layers (see Figure 1.16). These fluctuations can happen over a much larger scale than in a single atom, and the van der Waals bonding between such layers can therefore be much stronger than between atoms.

Several of the bonding types discussed here are identical to those relevant for the formation of molecules (with the exception of metallic bonding). They are therefore discussed in great depth in the literature for chemistry and molecular physics. A good overview on bonding in solids is given in:

Ibach, H. and Lüth, H. (2009). Solid State Physics, 4th edn. Springer.

Kittel, C. (2005). Introduction to Solid State Physics, 8th edn. John Wiley & Sons.

1 2.1 Why is a typical interatomic potential, such as the one in Figure 2.1, asymmetric?

2 2.2 Which elements are likely to form crystals through ionic bonding?

3 2.3 What types of forces are important for ionic bonding?

4 2.4 How does the lattice energy in an ionic crystal depend on the interatomic distance?

5 2.5 Explain the difference between cohesive energy and lattice energy.

6 2.6 Which elements are likely to form metals?

7 2.7 Where does the energy gain in metallic bonding come from?

8 2.8 What is the difference between a simple metal and a transition metal (definition and typical physical properties)?

9 2.9 Why is van der Waals bonding much weaker than most other bonding types?

1 2.1 Interatomic potential: Consider the model interatomic potential as a function of interatomic distance given by the equation(2.15) where and are parameters of the model.What is the physical origin of the strongly repulsive part of the potential?The Coulomb repulsion between the two nuclei.The increase of the electron energies due to the overlap of the electron clouds.What is the equilibrium distance between two atoms if their interaction is described by the potential in Eq. (2.15)?....What is the minimum value of ?

2 2.2 Cohesive energy: In an ionic solid, which energy is the largest?The cohesive energy.The lattice energy.Depends on the particular ionic solid.

3 2.3 Bonding and cohesive energy: When ordering the following elemental solids according to their cohesive energy (smallest to largest), which is the correct order?Pb, Ar, W.Ar, Pb, W.W, Pb, Ar.Ar, W, Pb.

4 2.4 Bonding type and structure: Which bonding types do typically lead to close‐packed crystal structures?Covalent bonding.Metallic bonding.Van der Waals bonding.A. and B.B. and C.

1 2.1 Ionic bonding: Calculate the potential energy for an ion in a sodium chloride crystal (the interatomic distance is 2.81 Å) in units of electron volts and joules. Neglect the influence of the repulsive potential. From this, calculate the lattice energy of sodium chloride and compare the result to the experimental value of 776 kJ . Also, calculate the cohesive energy in the same units.

2 2.2 Ionic bonding: The Madelung constant for a three‐dimensional NaCl crystal was given in Section 2.2. (a) Derive the Madelung constant analytically for a one‐dimensional NaCl chain as the one shown in Figure 2.5. (b)* Calculate the Madelung constant numerically for a one‐dimensional, two‐dimensional, and three‐dimensional NaCl lattice and plot the result as a function of the number of neighbor “shells” included in the computation. Compare the result for the one‐dimensional case to the analytical value from part (a). Figure 2.5 One‐dimensional chain of ions.