(2.2) 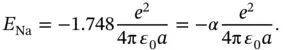
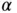 is called the Madelung constant.It is specific for a given structure (for the calculation of
is called the Madelung constant.It is specific for a given structure (for the calculation of 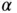 , see Problem 2). For calculating the electrostatic energy gain per mole, we have to multiply Eq. (2.2) by Avogadro's constant
, see Problem 2). For calculating the electrostatic energy gain per mole, we have to multiply Eq. (2.2) by Avogadro's constant 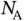 . We also have to multiply it by a factor of 2 to account for the fact that we have both Na and Cl ions in the solid. But at the same time, we have to divide it by 2 in order to avoid a double counting of bonds when we evaluate the electrostatic energy gain. So in the end, the energy gain per mole of NaCl is simply
. We also have to multiply it by a factor of 2 to account for the fact that we have both Na and Cl ions in the solid. But at the same time, we have to divide it by 2 in order to avoid a double counting of bonds when we evaluate the electrostatic energy gain. So in the end, the energy gain per mole of NaCl is simply 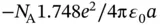 . Note that
. Note that 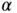 is larger than 1 so that the energy gain for forming a solid is higher than that for an isolated pair of ions. This is of course obvious since your salt shaker contains little crystals, not a molecular powder.
is larger than 1 so that the energy gain for forming a solid is higher than that for an isolated pair of ions. This is of course obvious since your salt shaker contains little crystals, not a molecular powder.
We can define the following contributions to the energy balance for forming the solid. The cohesive energyis the total energy difference between any solid and the isolated atoms it is made of. For an ionic crystal, the cohesive energy can be calculated in a simple way. First, we need to consider how much energy is incurred in turning the atoms into ions using the ionization energiesand electron affinitiesof the atoms. Next, the total electrostatic energy gain for the crystal needs to be calculated using the known crystal structure, as shown above for NaCl. This energy gain is called the lattice energy.The cohesive energy is then simply the lattice energy minus the energy needed to turn the atoms into ions (see Problem 1).
It might seem that we can calculate the cohesive energy for ionic solids from purely classical physics, but this is not correct. Note that we have used the experimental interatomic distance for the calculation of the lattice energy. The calculation of this distance would involve quantum mechanics because it contains the repulsive part of the potential. In fact, the presence of the repulsive potential also causes the actual potential minimum for a given interatomic distance 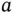 to be slightly shallower than expected from the pure Coulomb potential (by about 10%). This can be seen in Figure 2.1where the potential minimum lies above the Coulomb contribution to the potential at the equilibrium distance. In any event, ionic bonding is very strong. The cohesive energy per atom is on the order of several electron volts.
to be slightly shallower than expected from the pure Coulomb potential (by about 10%). This can be seen in Figure 2.1where the potential minimum lies above the Coulomb contribution to the potential at the equilibrium distance. In any event, ionic bonding is very strong. The cohesive energy per atom is on the order of several electron volts.
Covalent bonding is based on the sharing of electrons between different atoms. The simplest case is that of the hydrogen molecule, which we will discuss quantitatively below. In solids, covalent bonding is often found for elements with a roughly half‐filled outer shell. A prominent example is carbon, which forms solids such as diamond, graphene, and graphite as well as complex molecules such as buckminsterfullerene  or carbon nanotubes. The covalent bonds in diamond are constructed from linear combinations of the 2s orbital and three 2p orbitals. This results in four so‐called
or carbon nanotubes. The covalent bonds in diamond are constructed from linear combinations of the 2s orbital and three 2p orbitals. This results in four so‐called 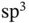 orbitals that stick out in a tetrahedral configuration from the carbon atoms. In graphene and graphite, the 2s orbital is combined with only two 2p orbitals, giving three
orbitals that stick out in a tetrahedral configuration from the carbon atoms. In graphene and graphite, the 2s orbital is combined with only two 2p orbitals, giving three 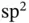 orbitals, all in one plane and separated by angles of
orbitals, all in one plane and separated by angles of 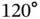 , and one p orbital oriented perpendicular to this plane. This linear combination of orbitals already reveals an important characteristic of covalent bonding: It is highly directional. In addition to this, it is also very stable and the cohesive energies for covalently bonded solids are typically several electron volts per atom.
, and one p orbital oriented perpendicular to this plane. This linear combination of orbitals already reveals an important characteristic of covalent bonding: It is highly directional. In addition to this, it is also very stable and the cohesive energies for covalently bonded solids are typically several electron volts per atom.
We study covalent bonding by the simplest example, the diatomic hydrogen molecule 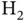 , with its two electrons. We denote the positions of the nuclei of the two hydrogen atoms as
, with its two electrons. We denote the positions of the nuclei of the two hydrogen atoms as 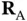 and
and 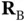 . In the following, we keep the nuclei fixed at these positions and denote the distance in between them by
. In the following, we keep the nuclei fixed at these positions and denote the distance in between them by 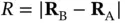 . The Hamiltonian for the hydrogen molecule can then be written as
. The Hamiltonian for the hydrogen molecule can then be written as
(2.3) 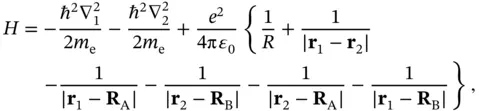
where 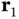 and
and 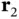 are the coordinates of the electrons belonging to nucleus A and B, respectively. The first two terms describe the kinetic energies of the two electrons. The operators
are the coordinates of the electrons belonging to nucleus A and B, respectively. The first two terms describe the kinetic energies of the two electrons. The operators  and
and 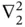 act only on the coordinates
act only on the coordinates 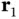 and
and 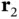 , respectively. The electrostatic term contains the repulsion between the two nuclei and the repulsion between the two electrons as well as the attraction between each electron and each nucleus.
, respectively. The electrostatic term contains the repulsion between the two nuclei and the repulsion between the two electrons as well as the attraction between each electron and each nucleus.
Calculating the energy eigenvalues and wave functions for this Hamiltonian is a formidable problem, mostly because of the interactions between the two electrons (the second term in the curly brackets). We shall return to this problem later. For now, we exploit the fact that the essence of covalent bonding can already be understood by considering just one electron, i.e. by simplifying Eq. (2.3) so that it describes the 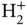 molecular ion:
molecular ion:
Читать дальше

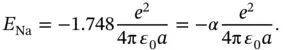
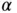 is called the Madelung constant.It is specific for a given structure (for the calculation of
is called the Madelung constant.It is specific for a given structure (for the calculation of 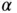 , see Problem 2). For calculating the electrostatic energy gain per mole, we have to multiply Eq. (2.2) by Avogadro's constant
, see Problem 2). For calculating the electrostatic energy gain per mole, we have to multiply Eq. (2.2) by Avogadro's constant 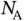 . We also have to multiply it by a factor of 2 to account for the fact that we have both Na and Cl ions in the solid. But at the same time, we have to divide it by 2 in order to avoid a double counting of bonds when we evaluate the electrostatic energy gain. So in the end, the energy gain per mole of NaCl is simply
. We also have to multiply it by a factor of 2 to account for the fact that we have both Na and Cl ions in the solid. But at the same time, we have to divide it by 2 in order to avoid a double counting of bonds when we evaluate the electrostatic energy gain. So in the end, the energy gain per mole of NaCl is simply 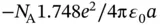 . Note that
. Note that 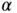 is larger than 1 so that the energy gain for forming a solid is higher than that for an isolated pair of ions. This is of course obvious since your salt shaker contains little crystals, not a molecular powder.
is larger than 1 so that the energy gain for forming a solid is higher than that for an isolated pair of ions. This is of course obvious since your salt shaker contains little crystals, not a molecular powder.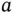 to be slightly shallower than expected from the pure Coulomb potential (by about 10%). This can be seen in Figure 2.1where the potential minimum lies above the Coulomb contribution to the potential at the equilibrium distance. In any event, ionic bonding is very strong. The cohesive energy per atom is on the order of several electron volts.
to be slightly shallower than expected from the pure Coulomb potential (by about 10%). This can be seen in Figure 2.1where the potential minimum lies above the Coulomb contribution to the potential at the equilibrium distance. In any event, ionic bonding is very strong. The cohesive energy per atom is on the order of several electron volts.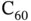 or carbon nanotubes. The covalent bonds in diamond are constructed from linear combinations of the 2s orbital and three 2p orbitals. This results in four so‐called
or carbon nanotubes. The covalent bonds in diamond are constructed from linear combinations of the 2s orbital and three 2p orbitals. This results in four so‐called 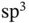 orbitals that stick out in a tetrahedral configuration from the carbon atoms. In graphene and graphite, the 2s orbital is combined with only two 2p orbitals, giving three
orbitals that stick out in a tetrahedral configuration from the carbon atoms. In graphene and graphite, the 2s orbital is combined with only two 2p orbitals, giving three 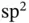 orbitals, all in one plane and separated by angles of
orbitals, all in one plane and separated by angles of 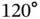 , and one p orbital oriented perpendicular to this plane. This linear combination of orbitals already reveals an important characteristic of covalent bonding: It is highly directional. In addition to this, it is also very stable and the cohesive energies for covalently bonded solids are typically several electron volts per atom.
, and one p orbital oriented perpendicular to this plane. This linear combination of orbitals already reveals an important characteristic of covalent bonding: It is highly directional. In addition to this, it is also very stable and the cohesive energies for covalently bonded solids are typically several electron volts per atom.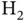 , with its two electrons. We denote the positions of the nuclei of the two hydrogen atoms as
, with its two electrons. We denote the positions of the nuclei of the two hydrogen atoms as 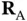 and
and 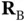 . In the following, we keep the nuclei fixed at these positions and denote the distance in between them by
. In the following, we keep the nuclei fixed at these positions and denote the distance in between them by 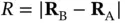 . The Hamiltonian for the hydrogen molecule can then be written as
. The Hamiltonian for the hydrogen molecule can then be written as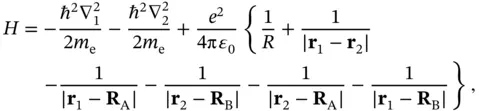
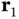 and
and 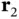 are the coordinates of the electrons belonging to nucleus A and B, respectively. The first two terms describe the kinetic energies of the two electrons. The operators
are the coordinates of the electrons belonging to nucleus A and B, respectively. The first two terms describe the kinetic energies of the two electrons. The operators  and
and 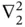 act only on the coordinates
act only on the coordinates 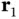 and
and 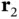 , respectively. The electrostatic term contains the repulsion between the two nuclei and the repulsion between the two electrons as well as the attraction between each electron and each nucleus.
, respectively. The electrostatic term contains the repulsion between the two nuclei and the repulsion between the two electrons as well as the attraction between each electron and each nucleus.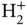 molecular ion:
molecular ion:










