There are, however, also solids that are not crystalline. These are called amorphous. The amorphous state is characterized by the absence of any long‐range order. There may exist, however, a degree of short‐range order between the atoms.
This chapter is divided into three parts. In the first part, we define some basic mathematical concepts needed to describe crystals. We keep things simple and mostly use two‐dimensional examples to illustrate the ideas. In the second part, we discuss common crystal structures. For the moment, we will not ask why the atoms bind together in the way they do – this topic will be discussed in Chapter 2. Finally, we delve into a more detailed discussion of X‐ray diffraction, the experimental technique that can be used to determine the microscopic structure of crystals. X‐ray diffraction is used not only in solid state physics but also for a wide range of problems in nanotechnology and structural biology.
1.1 General Description of Crystal Structures
Our description of crystals starts with the mathematical definition of the lattice. A lattice is a set of regularly spaced points with positions defined as multiples of generating vectors. In two dimensions, a lattice can be defined as all the points that can be reached by the vectors 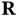 , created from two non‐collinear vectors
, created from two non‐collinear vectors  and
and  as
as
(1.1) 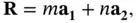
where  and
and 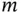 are integers. In three dimensions, the corresponding definition is
are integers. In three dimensions, the corresponding definition is
(1.2) 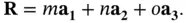
Such a lattice of points is also called a Bravais lattice. The number of possible Bravais lattices with different symmetries is limited to 5 in two dimensions and to 14 in three dimensions. An example of a two‐dimensional Bravais lattice is given in Figure 1.1. The lengths of the vectors  and
and  are often called the lattice constants.
are often called the lattice constants.
Having defined the Bravais lattice, we move on to the definition of the primitive unit cell. By this we denote any volume of space that, when translated through all the vectors of the Bravais lattice, will fill space without overlap and without leaving any voids. The primitive unit cell of a lattice contains only one lattice point. It is also possible to define nonprimitive unit cellscontaining several lattice points. These fill space without leaving voids when translated through a subset of the Bravais lattice vectors. Possible choices of a unit cell for a two‐dimensional rectangular Bravais lattice are illustrated in Figure 1.2. It is evident from the figure that a nonprimitive unit cell has to be translated by a multiple of one (or two) lattice vectors to fill space without voids and overlap. A special choice of the primitive unit cell is the Wigner–Seitz cell, which is also shown in Figure 1.2. It is the region of space that is closer to one given lattice point than to any other.
The last definition we need in order to describe an actual crystal is that of a basis. The basis describes the items we “put” on the lattice points, that is, the building blocks for the real crystal. The basis can consist of one or several atoms, or even of complex molecules as in the case of protein crystals. Different cases are illustrated in Figure 1.3.

Figure 1.1 A two‐dimensional Bravais lattice.

Figure 1.2 Illustration of (primitive and nonprimitive) unit cells and of the Wigner–Seitz cell for a rectangular two‐dimensional lattice.

Figure 1.3 A two‐dimensional Bravais lattice with different choices for the basis.
Finally, we add a remark about symmetry. So far, we discussed only translational symmetry. However, a real crystal may also exhibit point symmetry. Compare the structures in the middle and the bottom of Figure 1.3. The former structure possesses a number of symmetry elements that are missing in the latter – for example, mirror lines, a rotational axis, and inversion symmetry. The knowledge of such symmetries can be very useful for the description of crystal properties.
1.2 Some Important Crystal Structures
After this rather formal treatment, we look at a number of common crystal structures for different types of solids, such as metals, ionic solids, or covalently bonded solids. In Chapter 2, we will take a closer look at the details of the bonding in these types of solids.
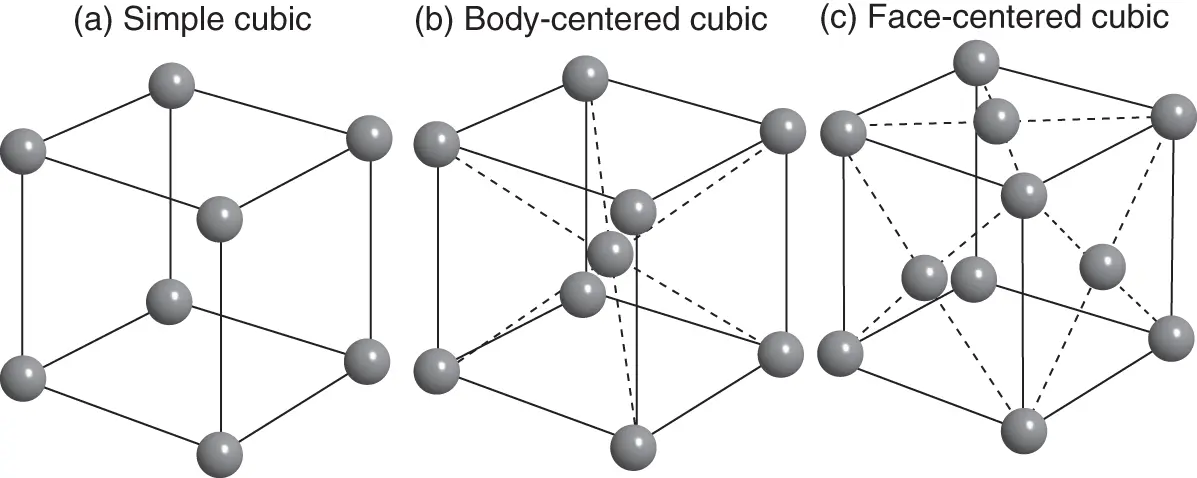
Figure 1.4 (a) Simple cubic structure; (b) body‐centered cubic structure; and (c) face‐centered cubic structure. Note that the spheres are depicted much smaller than in the situation of most dense packing and not all of the spheres on the faces of the cube are shown in (c).
We begin with one of the simplest crystal structures possible, the simple cubic structureshown in Figure 1.4a. This structure is not very common among elemental solids, but it is an important starting point for understanding many other structures. Only one chemical element (polonium) is found to crystallize in the simple cubic structure. The structure is unfavorable because of its openness – there are many voids, if we think of the atoms as solid spheres in contact with each other. In metals, which are the most common elemental solids, directional bonding is not important, and a close packing of the atoms is usually favored. We will learn more about this in the next chapter. For covalent solids, on the other hand, directional bonding is important, but six bonds extending from the same atom in an octahedral configuration is highly uncommon in elemental solids.
Читать дальше

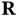 , created from two non‐collinear vectors
, created from two non‐collinear vectors  and
and  as
as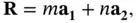
 and
and 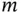 are integers. In three dimensions, the corresponding definition is
are integers. In three dimensions, the corresponding definition is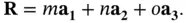
 and
and  are often called the lattice constants.
are often called the lattice constants.














