The multiple‐choice questions have only one correct answer, or, if several correct answers exist, there is an explicit option to choose this, e. g., “C. Both A. and B. are correct.” In some cases, there is an overlap between a “basic concepts” question testing a conceptual understanding of a subject and a “problem” with a more in‐depth treatment of the same question.
My thanks go to the 2021 class of the Statistical Physics and Solid State Physics course at Aarhus University for testing much of the new content, as well as to the teaching instructors Paulina Majchrzak, Alfred Jones, Michael Iversen and Nikolaj Rønne. I also thank Davide Curcio for introducing me to a new set of advanced writing tools and Charlotte E. Sanders for many helpful comments on the manuscript.
Physical Constants and Energy Equivalents
| Planck constant |
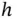 |
 J s J s |
|
|
 eV s eV s |
| Boltzmann constant |
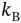 |
 J K J K 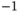 |
|
|
 eV K eV K 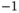 |
| Proton charge |
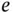 |
 C C |
| Bohr radius |
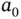 |
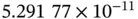 m m |
| Bohr magneton |
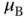 |
 J T J T 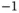 |
| Avogadro constant |
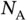 |
 mol mol 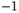 |
| Speed of light |
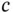 |
 m s m s 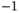 |
| Rest mass of the electron |
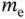 |
 kg kg |
| Rest mass of the proton |
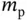 |
 kg kg |
| Rest mass of the neutron |
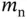 |
 kg kg |
| Atomic mass unit |
u |
 kg kg |
| Permeability of vacuum |
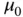 |
 V s A V s A  m m 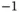 |
| Permittivity of vacuum |
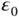 |
  J J  m m 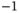 |
1 eV =  J
J
1 K =  eV
eV
Our general objective in this book is to understand the macroscopic properties of solids on a microscopic level. In view of the many particles in solids, coming up with any microscopic description appears to be a daunting task. It is clearly impossible to solve the equations of motion (classical or quantum‐mechanical) of the particles. Fortunately, it turns out that solids are often crystalline, with the atoms arranged on a regular lattice, and this symmetry permits us to solve microscopic models despite the vast number of particles involved. In a way, this situation is similar to atomic physics where the key to a quantum‐mechanical description is the spherical symmetry of the atom. We will often imagine a macroscopic solid as one single crystal, a perfect lattice of atoms without any defects whatsoever. While it may seem that such perfect crystals are not particularly relevant for real materials, this is in fact not the case. Many solids are actually composed of small crystalline grains. Such solids are called polycrystalline, in contrast to a macroscopic single crystal, but the number of atoms within a perfect crystalline environment in them is still very large compared to the number of atoms on the grain boundary. For instance, for a grain size on the order of 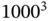 atomic distances, only about 0.1% of all atoms are at the grain boundaries.
atomic distances, only about 0.1% of all atoms are at the grain boundaries.
Читать дальше

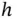
 J s
J s eV s
eV s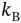
 J K
J K 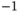
 eV K
eV K 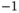
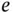
 C
C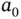
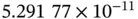 m
m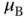
 J T
J T 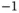
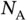
 mol
mol 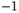
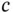
 m s
m s 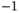
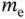
 kg
kg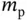
 kg
kg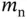
 kg
kg kg
kg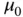
 V s A
V s A  m
m 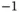
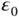

 J
J  m
m 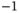
 J
J eV
eV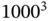 atomic distances, only about 0.1% of all atoms are at the grain boundaries.
atomic distances, only about 0.1% of all atoms are at the grain boundaries.










