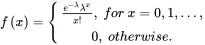 (1.17)
(1.17)
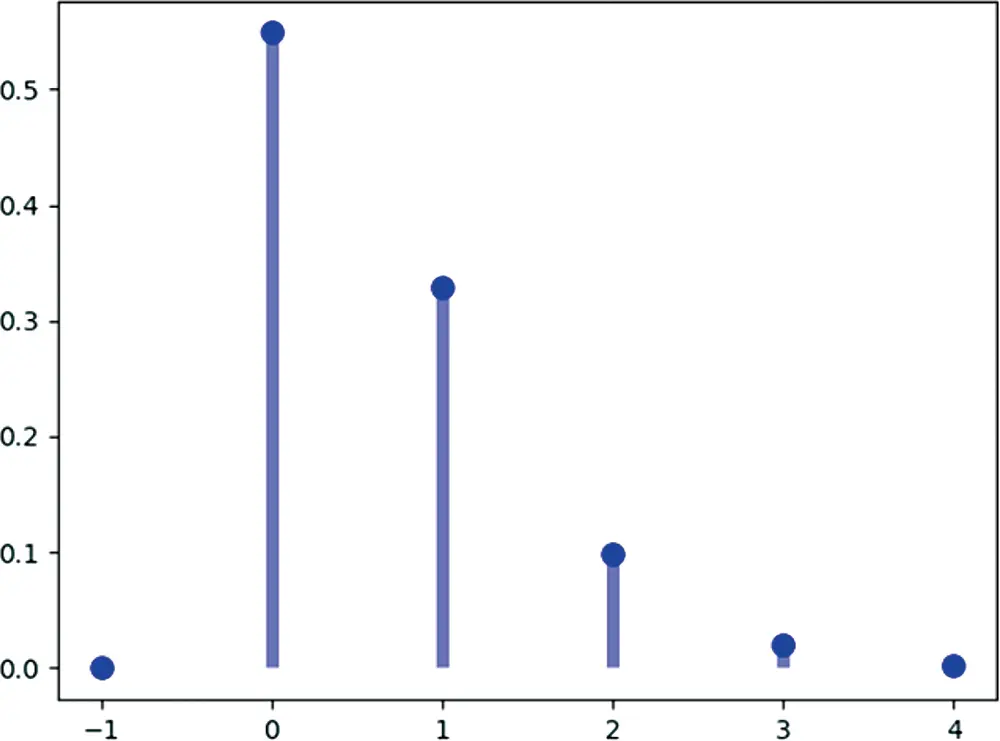
Figure 1.2 The pmf of the Poisson distribution with λ=0.6 .
The mean and variance of the Poisson distribution are
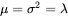 ((1.18)
((1.18)
1.2.2 Continuous Probability Distributions
We say that a random variable X has a continuous distribution or that X is a continuous random variable if there exists a nonnegative function f, defined on the real line, such that for every interval of real numbers (bounded or unbounded), the probability that X takes a value in an interval [a, b] is the integral of f over that interval, that is,
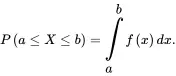 (1.19)
(1.19)
If X has a continuous distribution, the function f will be the probability density function (pdf) of X. The pdf must satisfy the following requirements:
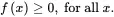 (1.20)
(1.20)
The cdf of a continuous distribution is given by
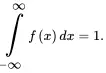 (1.21)
(1.21)
The mean, μ, and variance, σ2, of the continuous random variable are calculated by
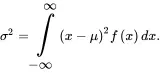 (1.22)
(1.22)
1.2.2.1 Exponential Distribution
A random variable T follows the exponential distribution if and only if the pdf (shown in Figure 1.3) of T is
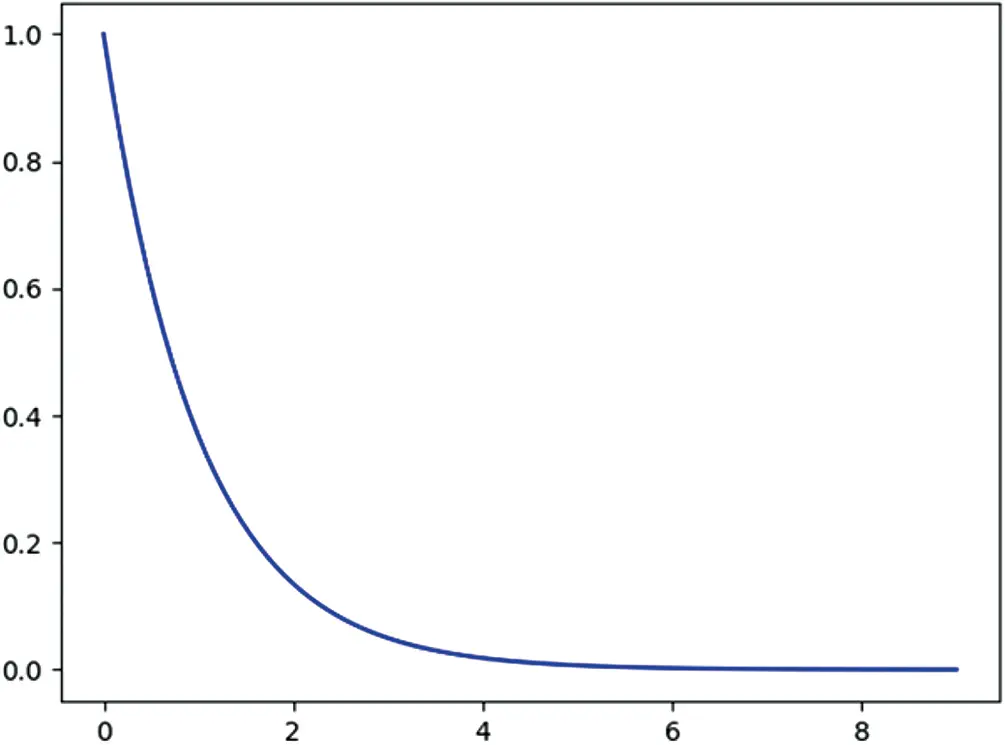
Figure 1.3 The pdf of the exponential distribution with λ=1.
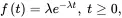 (1.23)
(1.23)
where λ>0 is the parameter of the distribution. The cdf of the exponential distribution is
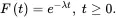 (1.24)
(1.24)
If T denotes the failure time of an item with exponential distribution, the reliability function will be
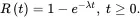 (1.25)
(1.25)
The hazard rate function is
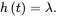 (1.26)
(1.26)
The mean, μ, and variance, σ2 are
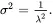 (1.27)
(1.27)
1.2.2.2 Weibull Distribution
A random variable T follows the Weibull distribution if and only if the pdf (shown in Figure 1.4) of T is
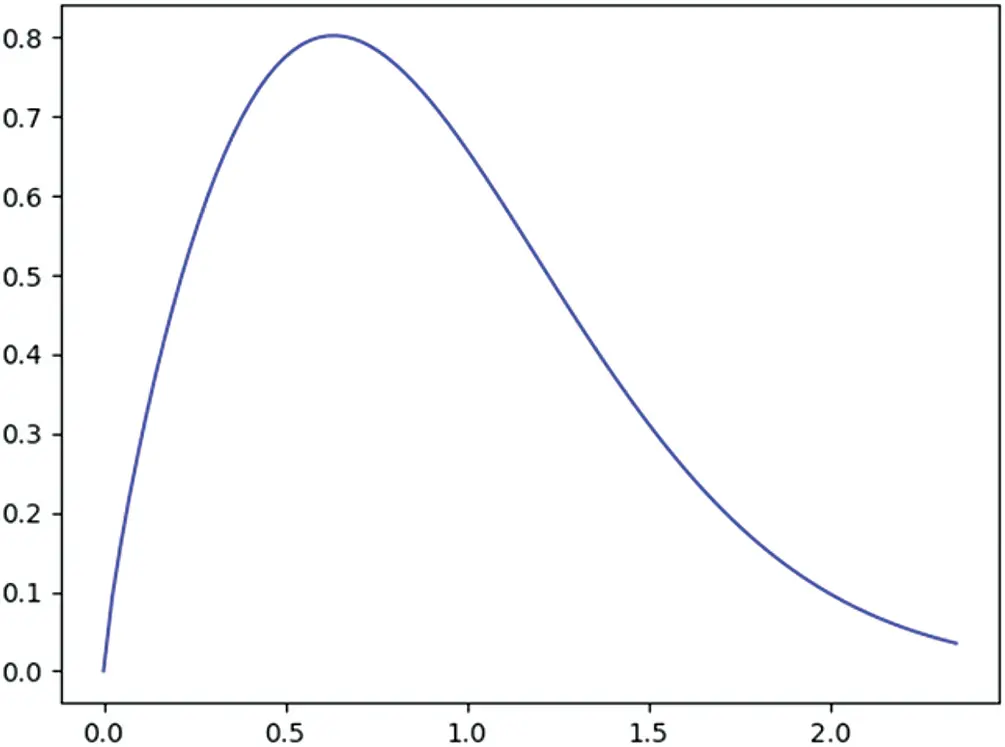
Figure 1.4 The pdf of the Weibull distribution with β=1.79, η=1.
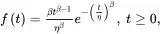 (1.28)
(1.28)
where β>0 is the shape parameter and η>0 is the scale parameter of the distribution. The cdf of the Weibull distribution is
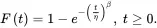 (1.29)
(1.29)
If T denotes the time to failure of an item with Weibull distribution, the reliability function will be
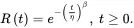 (1.30)
(1.30)
The hazard rate function is
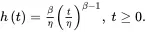 (1.31)
(1.31)
The mean, μ, and variance, σ2, are
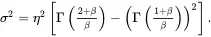 (1.32)
(1.32)
1.2.2.3 Gamma Distribution
A random variable T follows the gamma distribution if and only if the pdf (shown in Figure 1.5) of T is
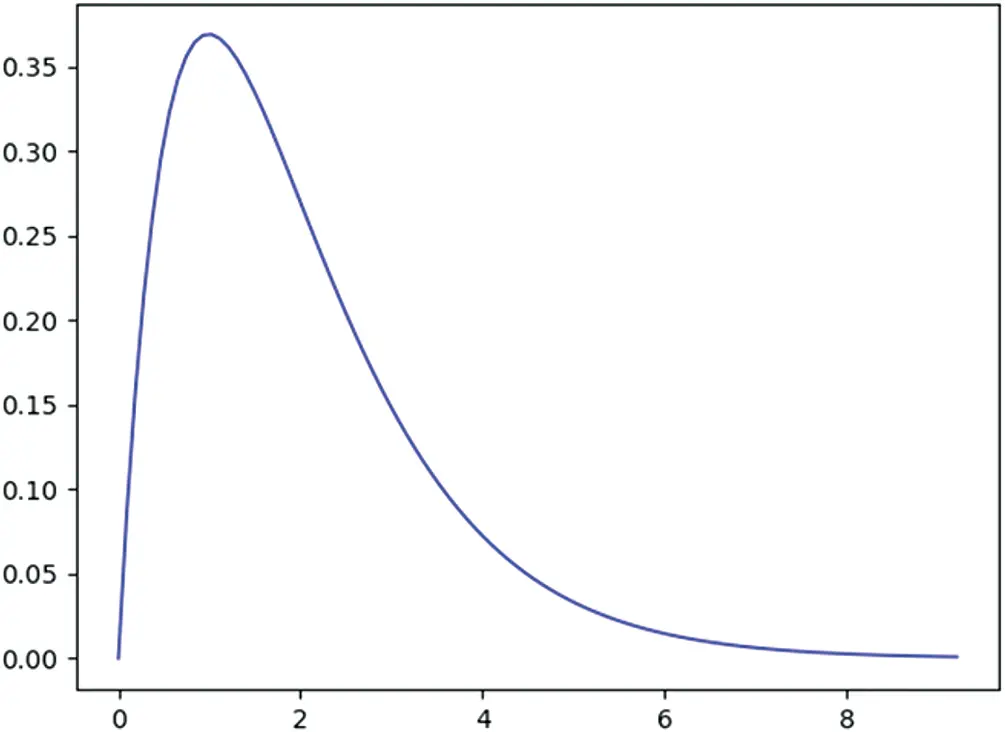
Figure 1.5 The pdf of the gamma distribution with β=1.99,λ=1 .
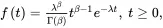 (1.33)
(1.33)
where β>0 is the shape parameter and η>0 is the scale parameter of the distribution. The cdf of the gamma distribution is
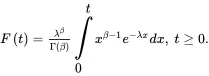 (1.34)
(1.34)
If T denotes the failure time of an item with gamma distribution, the reliability function will be
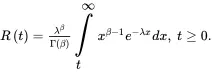 (1.35)
(1.35)
The hazard rate function is
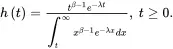 (1.36)
(1.36)
The mean, μ, and variance, σ2, are
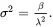 (1.37)
(1.37)
1.2.2.4 Lognormal Distribution
A random variable T follows the lognormal distribution if and only if the pdf (shown in Figure 1.6) of T is
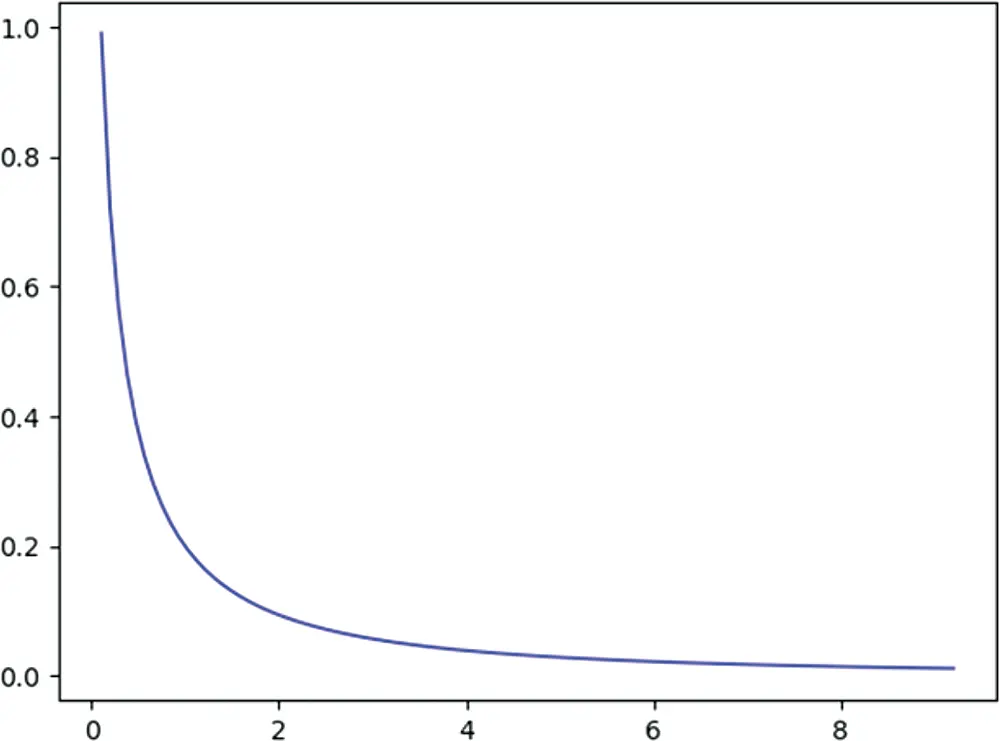
Figure 1.6 The pdf of the lognormal distribution with μ=0, σ=0.954 .
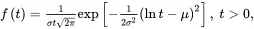 (1.38)
(1.38)
Читать дальше

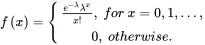 (1.17)
(1.17)
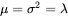 ((1.18)
((1.18)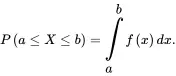 (1.19)
(1.19)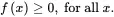 (1.20)
(1.20)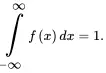 (1.21)
(1.21)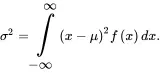 (1.22)
(1.22)
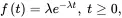 (1.23)
(1.23)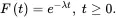 (1.24)
(1.24)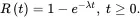 (1.25)
(1.25)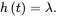 (1.26)
(1.26)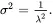 (1.27)
(1.27)
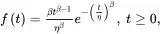 (1.28)
(1.28)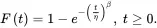 (1.29)
(1.29)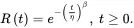 (1.30)
(1.30)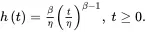 (1.31)
(1.31)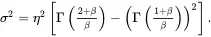 (1.32)
(1.32)
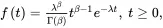 (1.33)
(1.33)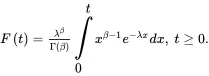 (1.34)
(1.34)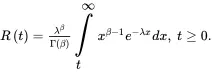 (1.35)
(1.35)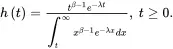 (1.36)
(1.36)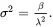 (1.37)
(1.37)
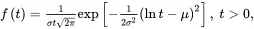 (1.38)
(1.38)