– Это съедобно?
– Нет.
– Это прозрачно?
– Нет.
– Это чашка?
– Да.
Игра: «найди число»
Вы с ребенком по очереди задумываете число от 1 до 100, а затем, чтобы его найти, задаете вопросы, на которые можно ответить только либо «Да», либо «Нет»:
– Я задумал число от 1 до 100.
– Оно четное?
– Да.
– Оно больше 50?
– Нет.
– Оно кратно 3?
– Да.
– Оно больше 25?
– Да.
И так далее.
Наилучшая стратегия в подобных играх (то есть та, которая быстрее всего позволит отгадать задуманное число) состоит в том, чтобы задавать такие вопросы, которые предполагали бы, что все оставшиеся возможные ответы разделяются на две равные группы, одна из которых имеет ответ «Да», а другая – «Нет». Поэтому «Это число четное?» отлично подходит на роль первого вопроса: половина возможных ответов является четной, а вторая половина – нет. С другой стороны, вопрос «Кончается ли это число на нуль?» не очень хорош, поскольку 90 из 100 чисел не заканчиваются на нуль и вероятность отрицательного ответа на этот вопрос весьма велика.
Сортировка и диаграммы Венна
В определенный момент в начальной школе ваш ребенок познакомится с двумя способами сортировки – при помощи диаграмм Венна(о которых вы, вероятно, слышали) и Кэрролла(с которыми вы, скорее всего, не сталкивались). Хотя оба способа позволяют сделать, в сущности, одно и то же, данные в них представляются немного по-разному и потому акцент делается на разных вещах.
Чтобы помочь ребенку освоить диаграммы Венна, можно организовать игру с двумя связанными петлей веревочками и набором различных предметов. Можно разложить на столе яблоко, апельсин, оранжевый восковой мелок и простой карандаш и исследовать возможные способы разбиения этого множества предметов на две группы. Это может быть группа съедобных вещей и группа оранжевых предметов. Ребенок быстро поймет, что некоторые вещи следует отнести к обеим группам: так, апельсин оранжевый и к тому же съедобен. Значит, две веревочных петли должны будут пересечься.
Кроме того, хотя это не очевидно на первый взгляд, существует и четвертое место, где могут находиться предметы, – пространство вокруг петель. В нашем примере то, что не оранжевое и невозможно съесть, должно будет остаться за пределами обоих групп.
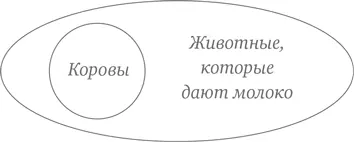
В начальной школе диаграмма Венна часто представляется только как пересечение двух контуров, но в некоторых ситуациях один из контуров может полностью находиться внутри другого. Так, если одна из петель представляет группу «животные, которые дают молоко», а вторая – группу «коровы», то, поскольку все коровы дают молоко, коровы полностью включены в группу молочных животных. Диаграмма Венна для этого случая становится похожей на яичницу-глазунью.
Кроме того, не существует правила, согласно которому петель (групп) должно быть обязательно две . Вы можете создать их столько, сколько нужно, чтобы представить все нужные вам категории, хотя в случае, когда групп больше трех, пересечения между ними сильно усложняются.
Этот вид диаграмм назван в честь автора «Алисы в Стране чудес», который занимался не только писательством, но и преподавал математику в Оксфорде. Чарльз Доджсон (настоящее имя Кэрролла) особенно интересовался логикой и в 1896 г. опубликовал книгу «Символическая логика» (Symbolic Logic), где представил диаграмму, названную им « двухбуквенной ». Позже этой диаграмме дали имя ее автора, и сегодня каждый учащийся начальной школы изучает диаграмму Кэрролла как метод категоризации объектов.
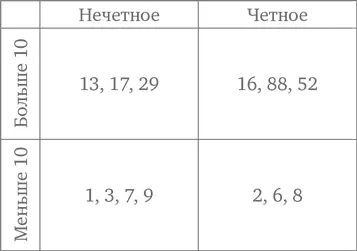
Особенно удобна диаграмма Кэрролла для группировки математических объектов. К примеру, карточки с числами можно рассортировать по самым разным признакам: четные/нечетные, больше/меньше 20, кратные/некратные пяти…
Проверьте себя
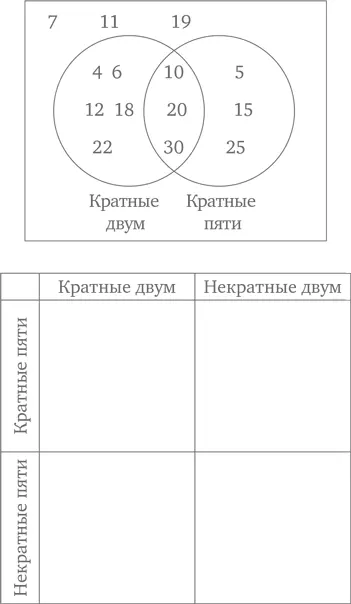
41. Диаграмма Кэрролла
Где на диаграмме Кэрролла оказались бы числа с приведенной ниже диаграммы Венна?
Проекты по обработке данных
Читать дальше
Конец ознакомительного отрывка
Купить книгу












![Роб Истуэй - Математика на ходу [Более 100 математических игр для больших и маленьких] [litres]](/books/406847/rob-istuej-matematika-na-hodu-bolee-100-matematich-thumb.webp)



