Роб Истуэй - Математика для мам и пап - Домашка без мучений

Простейший способ уяснить, что такое площадь, – представить себе ее как некий участок плоской поверхности. Площадь может быть застелена ковром, покрыта травой, оклеена обоями или покрашена, и ребенку нетрудно будет понять, что иногда площади приходится измерять, чтобы проверить, хватит ли на них ковра, краски и т. п.

Первый шаг ребенка на пути к измерению площади – пересчитывание квадратиков . Нарисовав фигуру на клетчатой бумаге, несложно (хотя довольно трудоемко) сосчитать, сколько в нее вошло квадратиков. Проще всего это сделать, безусловно, для прямоугольника.

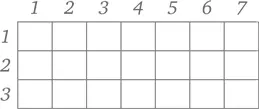
Тщательный подсчет позволит вам на практике убедиться в том, что в этом прямоугольнике уместился 21 квадратик. Но понимание того, что существует и более простой способ определить площадь прямоугольника, придет очень быстро. Здесь, к примеру, три строки по семь квадратиков, или семь столбиков по три квадратика, в любом случае площадь равна 3 × 7. Иными словами, нет никакой нужды считать квадратики поштучно, площадь прямоугольника можно найти, перемножив длины двух его сторон.

Метод счета квадратиков работает также для фигур любой другой формы, хотя не везде и не всегда вам встретятся удобные для счета целые квадратики. К примеру:

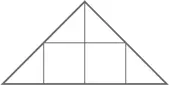
В этом треугольнике два целых квадратика и четыре половинки, что дает суммарно четыре полных квадратика.

Учащимся начальной школы редко предлагают считать что-то менее удобное, чем половинки квадратиков, но на самом деле эту идею можно развить. Существует правило, позволяющее довольно точно определить площадь: все неполные квадратики, в которых больше половины квадрата, считаются целыми , а все те, в которых меньше, – не считаются вообще. Таким образом, в треугольнике ниже присутствует шесть целых квадратиков и три с «более-чем-половиной», что дает нам площадь, равную девяти квадратикам.

Перед вами жуткая головоломка, в которой один квадратик площади возникает совершенно ниоткуда! Исходным материалом для нее служит обычная решетка размером 8 × 8 клеток и площадью соответственно 64 клетки.

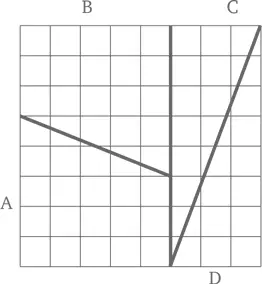
Вы видите, что решетка на рисунке разрезана на четыре части – A, B, C и D. Эти же самые части можно сложить иначе и получить следующий прямоугольник:

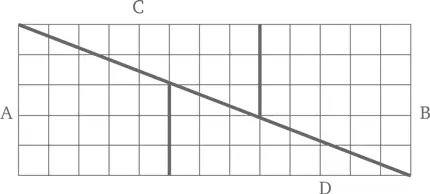
Убедитесь, что все части имеют в точности ту же форму, что и на первом рисунке. А теперь сосчитайте квадратики. Длина нашего прямоугольника составляет 13 клеток, ширина – 5. 13 раз по 5 будет 65… но это на единицу больше, чем в первоначальном квадрате. Откуда взялся лишний квадратик?

От учащихся начальной школы не требуется знание того, как вычисляется объем твердого тела. Тем не менее дети знакомятся с измерением объема жидкости в литрах; считается также, что они должны чувствовать и разумно оценивать, больше или меньше литра жидкости входит в конкретную емкость.

Несмотря на то что объем тела не будет рассматриваться в этом курсе сколько-нибудь подробно, полезно познакомить ребенка с некоторыми идеями, имеющими отношение к объему. Взяв два листа А4, можно провести интересный эксперимент.

Скатайте один лист вдоль длинной стороны, чтобы получилась длинная тонкая трубочка, а второй – вдоль короткой стороны, чтобы трубка получилась потолще и покороче.

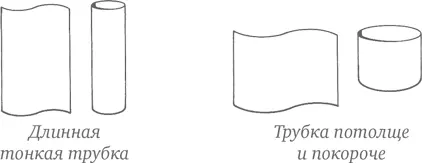
Эти две трубки имеют разную форму, но сделаны из одного и того же листа бумаги. В какую из них войдет больше гречневой крупы?

Если инстинкт говорит вам, что в каждый цилиндр должно поместиться одинаковое количество гречки, то он ошибается. В короткую широкую трубку входит больше – приблизительно на 40 %.