Роб Истуэй - Математика для мам и пап - Домашка без мучений

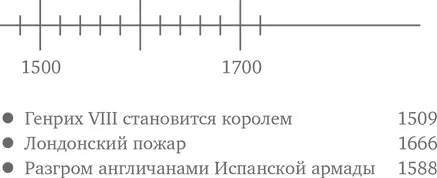
Как часто бывает на линейках, на этой между делениями, представляющими целые числа, есть более мелкие неподписанные деления. Считается, что пользователь должен сам их интерпретировать. В данном случае промежуток между соседними числами разделен на пять частей, так что каждое маленькое деление представляет 0,2. Длина отрезка в данном случае составляет 3,6 (то есть 4,6 минус 1,0).

Сможете ли вы сказать, почему при измерении отрезка на рисунке выше дети получили следующие неверные ответы?

4,6

4,3

3,3

В первом случае ребенок сосредоточился на правой границе отрезка и, соответственно, на большем числе (4,6) и не подумал проверить, находится ли левый конец отрезка на нулевой отметке линейки. Вообще, при использовании линейки часто не обойтись без простого вычитания, как здесь. (Вы можете познакомить ребенка с этой идеей, намеренно взяв сломанную линейку без нуля и задав ему вопрос: «О господи, как же нам измерить длину этой штуки?»)

Второй и третий неверные ответы возникли потому, что дети считывают положение правого конца отрезка как 4,3, то есть отсчитывают три маленьких деления и полагают, что каждое из них соответствует 0,1. Вы можете вовремя указать ребенку, что деления не могут равняться 0,1: достаточно аккуратно отсчитать по ним «4,1; 4,2; 4,3; 4,4…» и обнаружить, что пятое деление – которое вроде бы должно соответствовать 4,5 – совпадает с целым числом 5.

Во многих семьях принято выделять какой-то участок дверного косяка или стены, чтобы отслеживать на нем изменения роста ребенка. Как правило, дети радуются, когда обнаруживают в очередной раз, что немного выросли. Можно превратить этот уголок в объект постоянного интереса, если прикрепить к косяку или стене старую портновскую мерную ленту, чтобы дети могли по карандашной отметке сами определять свой рост.

Измерительные шкалы окружают нас со всех сторон – можно назвать хотя бы шкалы на весах, мерных кружках, термометрах и т. п. Конечно, шкала может быть размечена в целых единицах, но нисколько не реже встречаются шкалы, где промежуток между двумя соседними числами измеряется сотнями или небольшими десятичными дробями. Но какой бы ни была шкала, принципы ее чтения остаются одинаковыми: нужно научиться правильно интерпретировать промежутки между числами и понимать, что одно деление не всегда представляет одну единицу .

Чем лучше ваш ребенок научится читать дома всевозможные шкалы, тем проще ему будет интерпретировать новую, незнакомую шкалу, когда она ему попадется.

На рисунке – небольшой участок временно́й прямой, или оси времени. Любое событие можно отметить на ней стрелочкой, указывающей на определенный ее участок.

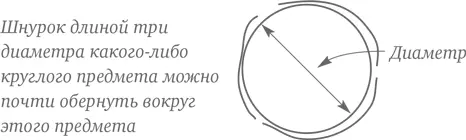
Слово «периметр» происходит от греческого слова περί (вокруг). Дети часто путают измерение периметра какого-то объекта и измерение его площади. Можно без труда избавиться от этой путаницы, если всегда связывать периметр с куском веревки. Какой длины кусок веревки вам потребуется, чтобы обернуть им данную окружность – или, к примеру, данный бассейн?

Периметр окружности имеет особое название: « длина окружности». Длина окружности круга при делении на его диаметр дает постоянную величину: это число, немногим большее трех, очень близкое к 3,14 и известное всем как число пи (или π). С ним дети не сталкиваются до средней школы, но вы можете познакомить сына или дочь с этим загадочным числом, обратив внимание ребенка на многочисленные круглые объекты в доме – банку фасоли, диск DVD или пиццу. Можно взять шнурок и наглядно продемонстрировать, что трех диаметров чуть-чуть, но не хватит на то, чтобы обкрутить им соответствующий предмет.

Эта фигура составлена из шести квадратов.

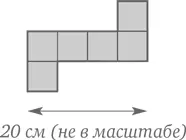
Вычислите периметр этой фигуры.