На ранних экземплярах таких «счетных дощечек» отметки стоят простым частоколом, хаотично, но на более поздних костях уже отмечается какая-то система, а со временем нормой становится группировка по пять штук.
Такой счет – простейший способ сбора и представления данных. Подсчет одновременно двух вещей – к примеру, очков, набранных каждой командой в игре мальчиков против девочек, – производится точно так же и позволяет с одного взгляда определить и количество, и соотношение этих двух вещей.
Иногда эта система счета используется просто для регистрации каких-то одинаковых вещей или событий – числа людей, пришедших на представление, или машин, заезжающих на парковку. Но составив табличку, можно одновременно отслеживать и несколько параметров: сгруппировать машины по маркам; выяснить, чипсы с какими ароматами пользуются наибольшим спросом; подсчитать число леденцов каждого цвета в разноцветной упаковке. Такие таблички известны как частотные таблицы; полученные с их помощью данные часто представляют в виде графиков и диаграмм, преобразовывая информацию в визуальную форму.
Сравнение, сортировка, систематизация
Это – три слона, на которых держится любая обработка информации. Взгляните на множество перечисленных в предыдущих главах способов, при помощи которых мы группировали и называли числа – целые числа, дроби, четные/нечетные, квадраты чисел, кратные, делители и т. п. Или припомните разнообразные типы и названия геометрических фигур: симметричные, двумерные или трехмерные, правильные и т. п.
В основе обработки информации лежит умение замечать общие свойства объектов и их различия , а затем распределять эти объекты по категориям.
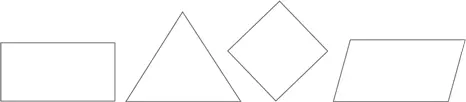
Которая из этих четырех фигур является здесь лишней?
Большинство людей сразу выберет треугольник, поскольку на данной картинке он единственная фигура с тремя сторонами. Но это лишь одна из возможных причин, по которым треугольник в этом наборе оказывается лишним. Как по-вашему, существуют ли другие объяснения? Прежде чем читать дальше, попробуйте назвать еще по крайней мере пять причин.
Вот некоторые:
• Его углы в сумме дают 180° (у каждой из остальных фигур сумма углов равна 360°).
• Он имеет три оси симметрии.
• У него самая маленькая площадь.
• У него самый маленький периметр.
• В нем три угла.
• Все его углы острые.
• Из шести таких треугольников можно сложить шестиугольник.
Треугольник не единственный возможный вариант ответа на вопрос «Какая фигура здесь лишняя?». В каждой из остальных фигур есть что-то, что ее выделяет: все, кроме одной, имеют равные стороны; все, кроме одной, имеют горизонтальное основание; у всех, кроме одной, все углы одинаковы… Это наглядно показывает, что классификация объектов редко бывает очевидной и однозначной. А поскольку при обработке информации постоянно требуется распределять информацию по категориям , то чем чаще ребенок будет придумывать и обдумывать всевозможные категории, тем лучше.
Игра: «Что здесь лишнее?»
Эта игра может стать увлекательным и творческим занятием для ребенка любого возраста. С маленькими детьми можно взять обычные бытовые предметы. Положите перед ним, к примеру, ложку, чашку, бутылку и вилку. Сможете ли вы вместе с сыном или дочкой найти критерии, по которым лишним в этой коллекции может быть назван каждый предмет по очереди? А если взять карандаш, пластмассовую линейку, фломастер и ластик? Кто из вас сможет найти самую необычную или глупую причину, по которой какой-то из этих предметов можно счесть лишним? Для начала приведем несколько примеров:
• Карандаш лишний, потому что только у него нет ни одной гибкой части.
• Линейка лишняя, потому что только она производит странный звук, если положить ее на край стола и щелкнуть по кончику
• Только у ластика есть другое название (стирательная резинка).
Дети постарше могут исследовать числовые множества. Сколько различных ответов можно дать на вопрос: «Какое число здесь лишнее: 20, 15, 24, 25?»?
Вариантом игры «Что здесь лишнее?» может стать игра «О чем я думаю?». Договоритесь, какого рода можно выбирать предметы. Скажем, обычные вещи, которые ребенок видит каждый день, – одежда на полке или посуда на столе. Можно вообразить и что-то из математики: целые числа меньше 100, трехмерные геометрические фигуры. Сможет ли ребенок определить, о чем вы думаете, задавая вопросы, предполагающие ответы «Да» или «Нет»? К примеру, на столе перед вами находятся чашка, стакан, сэндвич и яблоко:
Читать дальше
Конец ознакомительного отрывка
Купить книгу









![Роб Истуэй - Математика на ходу [Более 100 математических игр для больших и маленьких] [litres]](/books/406847/rob-istuej-matematika-na-hodu-bolee-100-matematich-thumb.webp)



