М. Нсанов - Цифровые устройства. Учебник для колледжей

Определим количество внешних соединений между элементами:

– в схеме рис. 2.25, построенной по исходной МДНФ: 8;

– в схеме рис. 2.40: 5.

Это подтверждает сказанное ранее: использование комбинированных ИМС уменьшает количество внешних соединений между элементами микросхем.

Подсчитаем аппаратурные затраты и задержку:

W = 4/6 + 4/5 = 0,67 + 0.8 = 1,47 корпуса; T = 4τ.

Полученные результаты сравним с этими же параметрами, характеризующими работу схемы рис. 2.25, построенной по исходной МДНФ:

W = 1,83 корпуса; T = 4τ.

Хорошо видно, что аппаратурные затраты уменьшились: 1,47 корпуса вместо 1,83.

Задержка вроде бы осталась той же: T = 4τ. Но соединительные линии внутри комбинированной микросхемы дают меньшую задержку сигналов, чем внешние соединения. Поэтому из-за уменьшения количества внешних соединений задержка на самом деле станет несколько меньше 4τ.

Сравнительный анализ качества схем, как уже было указано ранее, обычно производится по двум важнейшим критериям: задержке Tи аппаратурным затратам W.

Если не предъявляются заранее поставленные особые требования к отдельным критериям, то поступают следующим образом:

– Отбрасывают варианты, обладающие самыми худшими характеристиками или по T, или по W, или по обоим параметрам одновременно.

– Из других схем (все они образуют так называемое множество Парето ) отдают предпочтение более быстродействующим.

– В оставшихся вариантах с одинаковой минимальной задержкой выбирают наиболее экономичные схемы.

Для примера проведем сравнительную оценку качества схем, реализующих функцию Y 1, которые были построены нами различными способами. Для этого сведем данные по Tи W в небольшую таблицу (табл. 2.17).

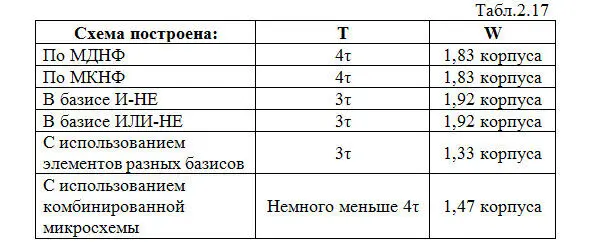
Сначала исключаем схемы, построенные по МДНФ и МКНФ, обладающие наибольшей задержкой. Затем исключаем схемы в базисах И-НЕи ИЛИ-НЕс наибольшими аппаратурными затратами.

В оставшихся двух вариантах, которые в данном случае и образуют множество Парето, выбираем как более быстродействующую схему, построенную с использованием элементов разных базисов.

Задана таблица истинности ЦУ, имеющего 4 входа (табл. 2.18).

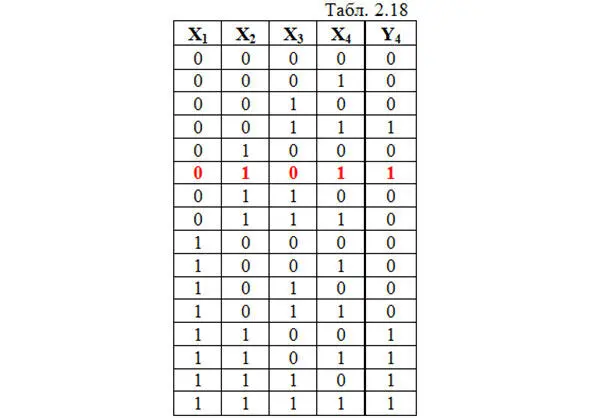
1. Записываем СДНФ:

Y 4= X 1′·X 2′·X 3·X 4\/ X 1′·X 2·X 3′·X 4\/ X 1·X 2·X 3′·X 4′ \/

\/ X 1·X 2·X 3′·X 4 \/ X 1·X 2·X 3·X 4′ \/ X 1·X 2·X 3·X 4.

2. Минимизируем СДНФ методом Вейча (рис. 2.41):

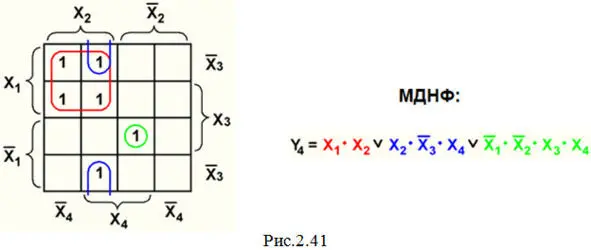
3. Подсчитываем требуемое количество элементов: 3 элемента НЕ +1 элемент 2И+1 элемент 3И+1 элемент 4И+2 элемента 2ИЛИ.

4. Подбираем микросхемы: по одной микросхеме КР1533ЛН1, КР1533ЛИ1, КР1533ЛИ3, КР1533ЛИ6, КР1533ЛЛ1.

5. Строим схему ЦУ в базисе И, ИЛИ, НЕ (рис. 2.42) и выполняем анализ ее работы в статическом режиме для одной комбинации входных сигналов (см. краснуюстроку в табл. 2.18).

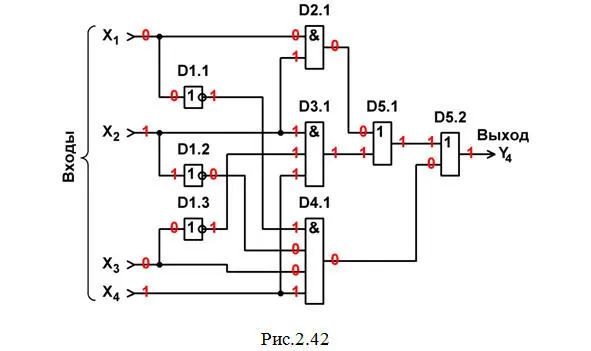
6. Составляем перечень элементов к этой схеме (табл. 2.19).

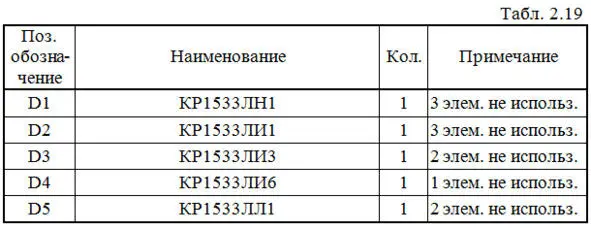
7. Определяем аппаратурные затраты и задержку:

W = 3/6 +1/4 +1/3 +1/2 +2/4 = 0,5 +0,25 +0,33 +0,5 +

+0,5 = 2,08 корпуса; T = 4τ.

8. Переходим к базису И-НЕ:

Y 4= [X 1·X 2\/ X 2·X 3′·X 4\/ X 1′·X 2′·X 3·X 4]′′ =

= [(X 1·X 2)′· (X 2·X 3′·X 4)′· (X 1′·X 2′·X 3·X 4)′]′ =

= [(X 1/ X 2) / (X 2/ X 3′ / X 4) / (X 1′ / X 2′ / X 3/ X 4)].

9. Подсчитываем требуемое количество элементов: 4 элемента 2И-НЕ(из них 3 элемента – для отрицания Х 1, Х 2и Х 3) +2 элемента 3И-НЕ+1 элемент 4И-НЕ.

10. Подбираем микросхемы: по одной микросхеме КР1533ЛА3, КР1533ЛА4 и КР1533ЛА1.

11. Строим схему ЦУ в базисе И-НЕ(рис. 2.43) и выполняем анализ ее работы в статическом режиме для одной комбинации входных сигналов та (см. краснуюстроку в табл. 2.18).