М. Нсанов - Цифровые устройства. Учебник для колледжей

W = 1 + 1/3 = 1 + 1,33 = 1,33 корпуса; T = 3τ.

Пример 3. МДНФ (см. пример 3 из темы 2.2):

Y 3= X 3′ \/ X 1′·X 2.

Переходим к базису И-НЕ:

Y 3= (X 3′ \/ X 1′·X 2)′′ = [(X 3′)′ \/ (X 1′·X 2)′]′ = (X 3) / (X 1′ / X 2).

Обратим внимание, что в МДНФ переменная была с отрицанием, затем после применения закона де Моргана у нее появилось второе отрицание, что по закону двойной инверсии дает прямое значение X 3. На будущее следует иметь в виду весьма простое правило: если в логическом выражении базиса И, ИЛИ, НЕ имеется минтерм, содержащий только одну переменную, то при переходе к базису И-НЕэта переменная будет обязательно менять свое значение на противоположное: если она была без отрицания, то будет с отрицанием; если же она была с отрицанием, то будет без него.

Подсчитываем требуемое количество элементов: 3 элемента 2И-НЕ(из них – 1 элемент для логического отрицания).

Подбираем микросхему: одна микросхема КР1533ЛА3.

Строим схему ЦУ в базисе И-НЕ (рис.2.34):

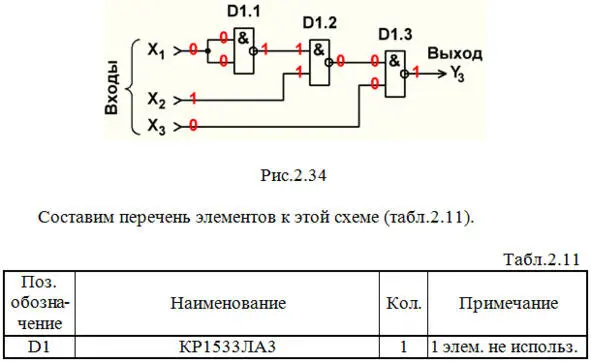
Выполним анализ работы ЦУ в статическом режиме для одной комбинации входных сигналов (см. рис.2.34 и краснуюстроку в табл.2.2).

Определим аппаратурные затраты и задержку:

W = 3/4 = 0,75 корпуса; T = 3τ.

Аналогично описанному в предыдущем параграфе переходу к базису И-НЕот МДНФ производится переход к базису ИЛИ-НЕ, только теперь уже от МКНФ:

1. Используется закон двойного отрицания(двойной инверсии):

A = A′′

2. Применяется вторая форма закона де Моргана:

(B·C·D·…)′ = B′ \/ C′ \/ D′ \/…

3. Полученное логическое выражение рекомендуется записать с использованием символа «стрелка Пирса» (смотрите табл.1.1), например:

(X 1\/ X 2)′ = X 1↓ X 2.

П р и м е ч а н и е :

В итоговом логическом выражении должны содержаться только операции ИЛИ-НЕ. Но кроме них, как правило, остаются все-таки операции НЕ, которые в данном случае следует выполнять с помощью элементов 2ИЛИ-НЕпутем объединения входов этих элементов.

Пример 1. МКНФ (см. пример 4 из темы 2.2):

Y 1= (X 1\/ X 2′) · (X 2′ \/ X 3) · (X 1′ \/ X 2\/ X3′).

Переходим к базису ИЛИ-НЕ. Для этого сначала используем закон двойного отрицания:

Подсчитываем требуемое количество элементов: 5 элементов 2ИЛИ-НЕ(из них 3 элемента – для отрицания) +2 элемента 3ИЛИ-НЕ.

Подбираем микросхемы: две микросхемы КР1533ЛЕ1 и одна микросхема КР1533ЛЕ4.

Строим схему ЦУ в базисе ИЛИ-НЕ(рис.2.35).

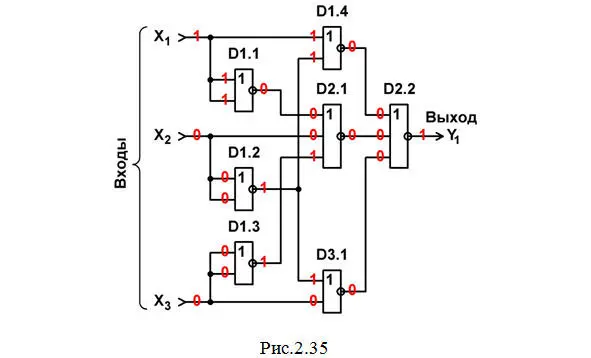
Составляем перечень элементов к этой схеме (табл.2.12).

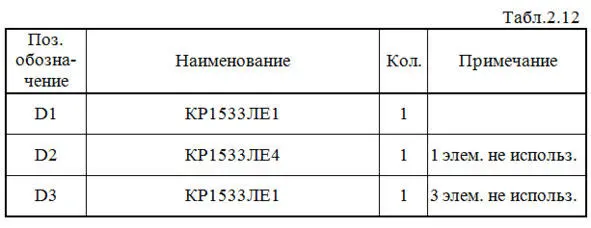
Выполним анализ работы ЦУ в статическом режиме для одной комбинации входных сигналов (см. рис.2.35 и синююстроку в табл.2.1).

Определим аппаратурные затраты и задержку:

W = 1 + 2/3 + 1/4 = 1 + 0,67 + 0,25 = 1,92 корпуса; T = 3τ.

Пример 2. МКНФ (см. пример 5 из темы 2.2):

Y 2= (X 1\/ X 3′) · (X 1′ \/ X 3) · (X 1′ \/ X 2).

Переходим к базису ИЛИ-НЕ:

Y 2= [(X 1\/ X 3′) · (X 1′ \/ X 3) · (X 1′ \/ X 2)]′′ =

= [(X 1\/ X 3′) ′ \/ (X 1′ \/ X 3) ′ \/ (X 1′ \/ X 2)′]′ =

= (X 1↓ X 3′) ↓ (X 1′ ↓ X 3) ↓ (X 1′ ↓ X 2).

Подсчитываем требуемое количество элементов: 5 элементов 2ИЛИ-НЕ(из них 2 элемента – для отрицания) +1 элемента 3ИЛИ-НЕ.

Подбираем микросхемы: две микросхемы КР1533ЛЕ1 и одна микросхема КР1533ЛЕ4.

Строим схему ЦУ в базисе ИЛИ-НЕ (рис.2.36).

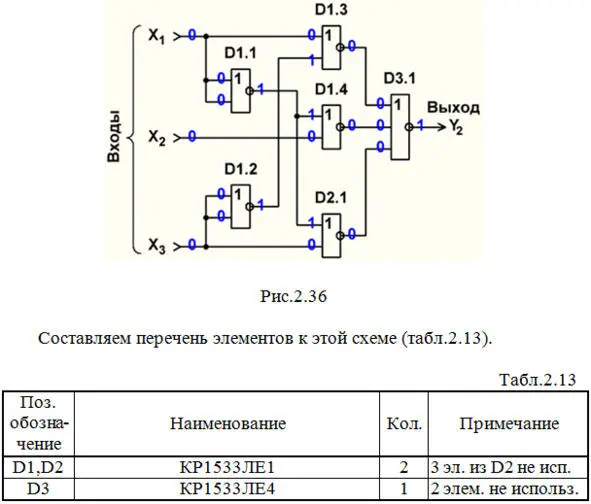
Выполним анализ работы ЦУ в статическом режиме для одной комбинации входных сигналов (см. рис.2.36 и синююстроку в табл.2.2).