М. Нсанов - Цифровые устройства. Учебник для колледжей

Аппаратурные затраты W обычно определяются количеством используемых корпусов микросхем (значение ряда других параметров – потребляемой мощности, надежности и др. – допустимо считать приблизительно пропорциональными W). В данном случае мы берем:

– 3 элемента НЕ из микросхемы КР1533ЛН1, которая содержит в целом 6 элементов; то есть используем 3/6 = 0,5 корпуса ИМС;

– 1 элемент 3Ииз микросхемы КР1533ЛИ3 (здесь всего – 3 элемента), т.е. используем 1/3 = 0,33 корпуса ИМС;

– 2 элемента 2Ииз микросхемы КР1533ЛИ1, содержащей в целом 4 элемента; т.е. используем 2/4 = 0,5 корпуса ИМС;

– 2 элемента 2ИЛИиз микросхемы КР1533ЛЛ1, которая содержит всего 4 элемента; т.е. используем 2/4 = 0,5 корпуса ИМС.

Итого величина аппаратурных затрат получается равной:

W = 0,5 + 0,33 + 0,5 + 0,5 = 1,83 корпуса.

П р и м е ч а н и е: лишние элементы частично занятых корпусов микросхем не учитываются, поскольку они могут быть использованы в других узлах.

Наряду с аппаратурными затратами очень важным критерием качества схем является задержка Т. В схемах, построенных с помощью микросхем средней степени интеграции, задержка достаточно объективно оценивается средним временем задержки распространения сигнала t P(см. §1.6) входящих в нее элементов по максимально длинному пути сигналов от входа к выходу. В рамках одной серии обычно полагают, что задержка любого логического элемента равна некоторой усредненной для данной серии величине τ, которая вместе с t Pнепосредственно элемента включает в себя и приближенную задержку на линиях связи между элементами. Для микросхем серии КР1533 значение τможно принять равным 8 нс.

Рассмотрим все возможные пути прохождения сигналов по схеме (рис.2.14) от входов к выходу и определим соответствующую величину задержки:

– со входа Х 1через 3 элемента – D2.1, D4.1 и D4.2, поэтому

Т = 3τ = 3·8 = 24 нс;

– со входа Х 1через 4 элемента – D1.1, D3.1, D4.1 и D4.2 (этот путь на рис.2.24 выделен жирной синейлинией);

Т = 4τ = 4·8 = 32 нс;

– со входа Х 2через 3 элемента – D2.1, D4.1 и D4.2;

Т = 3τ = 3·8 = 24 нс;

– со входа Х 2через 4 элемента – D1.2, D3.1, D4.1 и D4.2;

Т = 4τ = 4·8 = 32 нс;

– со входа Х 3через 3 элемента – D2.1, D4.1 и D4.2;

Т = 3τ = 3·8 = 24 нс;

– со входа Х 3через 3 элемента – D1.3, D3.2 и D4.2;

Т = 3τ = 3·8 = 24 нс.

Таким образом, для данной схемы максимальная задержка составляет Т = 4τ = 4·8 = 32 нс.

П р и м е ч а н и е. Строго говоря, полученное численное значение (в данном случае 32 нс) особого значения не имеет, так как задержка (да и аппаратурные затраты тоже) используются в основном для сравнительной оценки качества различных вариантов схем одного и того же ЦУ. Кроме этого, схема может строиться не на микросхемах логических элементов, а включаться целиком в состав какой-либо другой микросхемы, что приведет к существенному уменьшению задержки из-за сокращения линий связи между элементами внутри микросхемы, выполненной по интегральной технологии. Поэтому в большинстве случаев достаточно оперировать величиной Т = 4τ, не указывая его численное значение.

Приведем ряд других примеров, но уже без подробных пояснений.

Пример 2. МДНФ (см. пример 2 из §2.2):

Y2 = X1′·X3′ \/ X1·X2·X3.

Подсчитываем требуемое количество элементов: 2 элемента НЕ +1 элемент 2Ии 1 элемент 3И+1 элемент 2ИЛИ.

Подбираем микросхемы: по одной микросхеме КР1533ЛН1, КР1533ЛИ1, КР1533ЛИ3 и КР1533ЛЛ1.

Строим схему ЦУ в базисе И, ИЛИ, НЕ (рис.2.26).

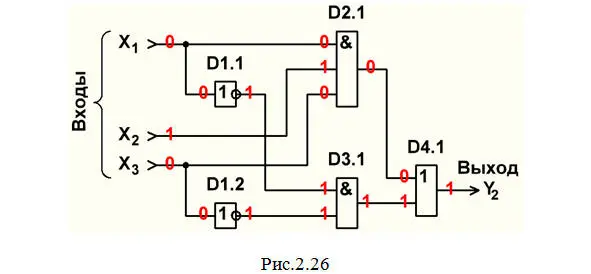
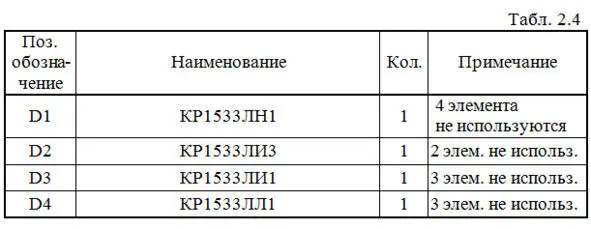
Составляем перечень элементов к этой схеме (табл.2.4).

Выполним анализ работы ЦУ в статическом режиме для одной комбинации входных сигналов (см. рис.2.26 и краснуюстроку в табл.2.2).

Определим аппаратурные затраты и задержку:

W = 2/6 + 1/3 + 1/4 + 1/4 = 0,33 + 0,33 + 0,25 + 0,25 =