М. Нсанов - Цифровые устройства. Учебник для колледжей

Переход выполняется в следующем порядке (под буквами А, B, C, Dи т. д. понимаются логические сигналы 0 или 1, а также любые логические операции и выражения, дающие в результате опять же сигналы 0 или 1):

1. Используется закон двойного отрицания (двойной инверсии):

A = A′′.

Справедливость этого закона проверить несложно, если вместо А подставить 0 или 1.

2. Применяется первая форма закона де Моргана :

(B \/ C \/ D \/ …)′ = B′·C′·D′·…

Правильность и этого закона тоже проверить несложно, если вместо В, С, Dи т. д. подставить любую комбинацию сигналов 0 и 1.

3. Полученное логическое выражение рекомендуется записать с использованием символа «штрих Шеффера» (смотрите табл.1.1), например:

(X1·X2)′ = X1 / X2.

Пример 1. МДНФ (см. пример 1 из темы 2.2):

Y 1= X 1′·X 2′ \/ X 2′·X 3′ \/ X 1·X 2·X 3.

Переходим к базису И-НЕ. Для этого сначала используем закон двойного отрицания:

Определяем требуемое количество элементов с учетом нужного количества входов у каждого элемента:

– для выполнения операций логического отрицания сигналов X 1, X 2и X 3берем три элемента 2И-НЕ(смотрите П р и м е ч а н и е выше);

– чтобы выполнить операцию в первой скобке, следует использовать элемент 2И-НЕ, так как в данной операции участвуют два сигнала: X 1′и X 2′;

– для реализации операции во второй скобке нужен элемент 2И-НЕ, потому что здесь в операции тоже участвуют два сигнала: X 2′и X 3′;

– чтобы выполнить операцию в третьей скобке, придется взять элемент 3И-НЕ, так как в данной операции участвуют три сигнала: X 1, X 2и X 3;

– и последним мы должны поставить элемент 3И-НЕ, потому что на его входы будут поступать три сигнала, являющиеся результатами операций в трех скобках.

Всего в схеме ЦУ: 5 элементов 2И-НЕ(напомним, что из них – три элемента для выполнения логического отрицания!) +2 элемента 3И-НЕ.

Подбираем микросхемы. Элементы 2И-НЕимеются в составе микросхемы КР1533ЛА3 (см. рис. 1.13), содержащей 4 элемента 2И-НЕ; так как нам требуется 5 таких элементов, то придется взять две микросхемы КР1533ЛА3, причем в одной из них три элемента использоваться не будут. Элементы 3И-НЕвходят в состав микросхемы КР1533ЛА4 (см. рис. 1.14), содержащей 3 элемента 3И-НЕ; нам нужны два элемента, поэтому достаточно использовать одну микросхему КР1533ЛА4, причем один элемент данной ИМС оказывается лишним.

Строим схему ЦУ в базисе И-НЕ(рис. 2.32).

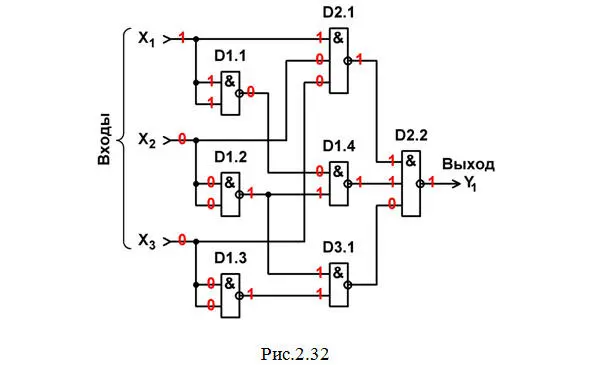
На этом же рис.2.32 выполнен анализ работы схемы ЦУ в статическом режиме для одной комбинации входных сигналов (см. краснуюстроку в табл. 2.1).

Составляем перечень элементов к этой схеме (табл.2.9).

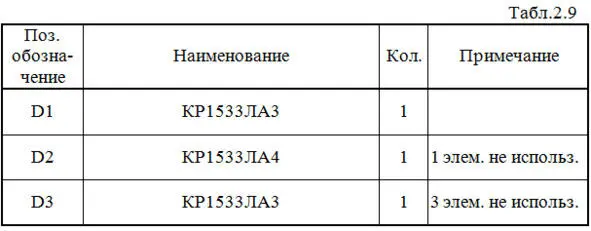
Определим аппаратурные затраты и задержку:

W = 1 + 2/3 + 1/4 = 1 + 0,67 + 0,25 = 1,92 корпуса; T = 3τ.

Пример 2. МДНФ (см. пример 2 из темы 2.2):

Y2 = X1′·X3′ \/ X1·X2·X3.

Переходим к базису И-НЕ:

Y2 = [(X1′·X3′) \/ (X1·X2·X3)]′′ = [(X1′·X3′)′· (X1·X2·X3)′]′ =

= [(X1′/X3′) / (X1/X2/X3)].

Подсчитываем требуемое количество элементов: 4 элемента 2И-НЕ(из них – 2 элемента для выполнения логического отрицания) +1 элемент 3И-НЕ.

Подбираем ИМС: по одной ИМС КР1533ЛА3 и КР1533ЛА4.

Строим схему ЦУ в базисе И-НЕ(рис.2.33).

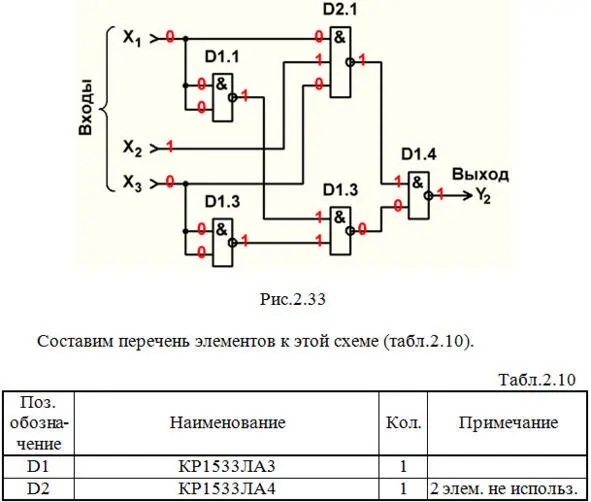
Выполним анализ работы ЦУ в статическом режиме для одной комбинации входных сигналов (см. рис.2.33 и краснуюстроку в табл.2.2).

Определим аппаратурные затраты и задержку: