М. Нсанов - Цифровые устройства. Учебник для колледжей

Определим аппаратурные затраты и задержку:

W = 1 + 1/4 + 1/3 = 1 + 0,25 + 0,33 = 1,58 корпуса; Т = 3τ.

Пример 3. МКНФ (см. пример 6 из темы 2.2):

Y 3= (X 2\/ X 3′) · (X 1′ \/ X 3′).

Переходим к базису ИЛИ-НЕ:

Y 3= [(X 2\/ X 3′) · (X 1′ \/ X 3′)]′′ = [(X 2\/ X 3′)′ \/ (X 1′ \/ X 3′)′]′ =

= [(X 2↓ X 3′) ↓ (X 1′ ↓ X 3′)].

Подсчитываем требуемое количество элементов: 5 элементов 2ИЛИ-НЕ(из них 2 элемента – для отрицания).

Подбираем микросхемы: две микросхемы КР1533ЛЕ1.

Строим схему ЦУ в базисе ИЛИ-НЕ(рис.2.37).

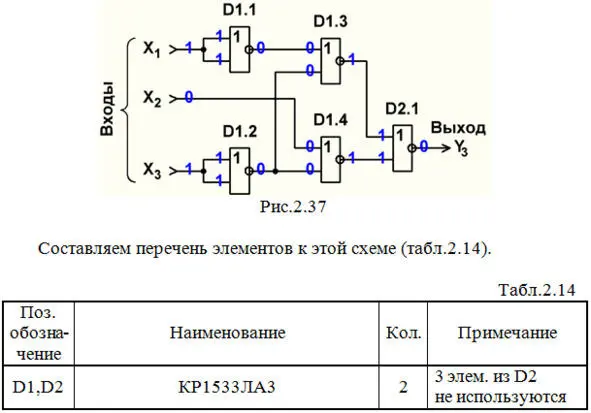
Выполним анализ работы ЦУ в статическом режиме для одной комбинации входных сигналов (см. рис.2.37 и синюю строку в табл.2.2).

Определим аппаратурные затраты и задержку:

W = 1 + 1/4 = 1 + 0,25 = 1,25 корпуса; T = 3τ.

Очень часто для достижения лучшего быстродействия или уменьшения аппаратурных затрат в схемах цифровых устройств используют элементы разных базисов. Приведем пример:

Пример 1. МКНФ (см. пример 4 из темы 2.2):

Y 1= (X 1\/ X 2′) · (X 2′ \/ X 3) · (X 1′ \/ X 2\/ X3′).

В данном логическом выражении базиса И, ИЛИ, НЕ преобразуем последний многочлен с использованием закона двойного отрицания и первого закона де Моргана:

(X 1′ \/ X 2\/ X 3′) = (X 1′ \/ X 2\/ X 3′)′′ = (X 1′)′· (X 2)′· (X 3′)′ =

= X 1/ X 2′ / X 3.

Теперь с учетом полученного результата исходное логическое выражение примет вид:

Y 1= (X 1\/ X 2′) · (X 2′ \/ X 3) · (X 1/ X 2′ / X 3).

Определим требуемое количество элементов: 1 элемент НЕ + 2 элемента 2ИЛИ+1 элемент 3И-НЕ(для выполнения операции в третьей скобке) +1 элемент 3И.

Подбираем микросхемы: по одной микросхеме КР1533ЛН1, КР1533ЛЛ1, КР1533ЛА4 и КР1533ЛИ3.

Строим схему ЦУ (рис. 2.38):

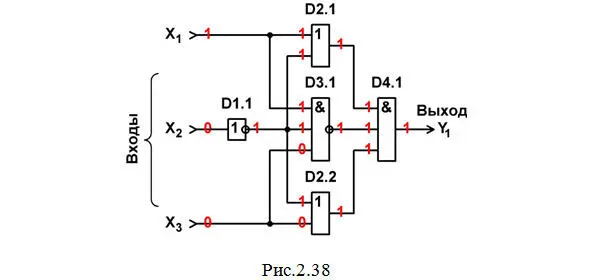
Составим перечень элементов к этой схеме (табл. 2.15).

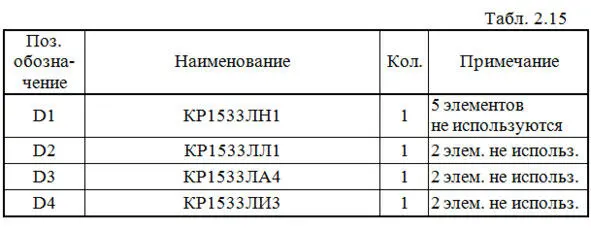
Выполним анализ работы ЦУ в статическом режиме для одной комбинации входных сигналов (см. рис.2.38 и краснуюстроку в табл.2.1).

Определим аппаратурные затраты и задержку:

W = 1/6 + 2/4 + 1/3 + 1/3 = 0,17 + 0,5 + 0,33 + 0,33 =

= 1,33 корпуса; T = 3τ.

Полученные результаты сравним с этими же параметрами, характеризующими работу схемы рис. 2.27, построенной по исходной МКНФ:

W = 1,83 корпуса; T = 4τ.

Хорошо видно, что преобразование только лишь одного многочлена МКНФ и вытекающая из этого необходимость использования в схеме элементов разных базисов привело: во-первых, к уменьшению задержки ( 3τвместо 4τ); и, во-вторых, к уменьшению аппаратурных затрат ( 1,33 корпуса вместо 1,83).

Иногда для достижения тех же целей увеличения быстродействия, уменьшения аппаратурных затрат, но в основном для уменьшения количества внешних соединений (то есть таких соединений, которые выполняются не внутри микросхемы, а снаружи путем монтажа) между микросхемами и элементами микросхем применяют комбинированные ИМС (смотрите, например, рис. 1.15 из параграфа 1.5). Приведем пример:

Пример 2. МДНФ (см. пример 1 из темы 2.2):

Y1 = X 1′·X 2′ \/ X 2′·X 3′ \/ X 1·X 2·X 3.

Логическое отрицание, как и в указанном примере 1 из темы 2.2, будем делать с помощью тех же элементов НЕ из микросхемы КР1533ЛН1. А для выполнения остальных операций воспользуемся микросхемой КР1533ЛР13 (рис. 2.39).

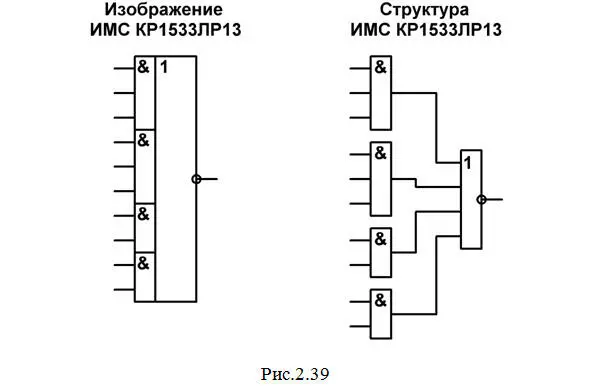
Но здесь нужно учесть, что в данной микросхеме на выходе стоит элемент ИЛИ-НЕ, поэтому выходной сигнал получится инвертированным. Чтобы получить на выходе все-таки прямое значение сигнала, выполним его повторное отрицание с помощью еще одного элемента НЕ из микросхемы КР1533ЛН1.

Строим схему ЦУ (рис. 2.40):

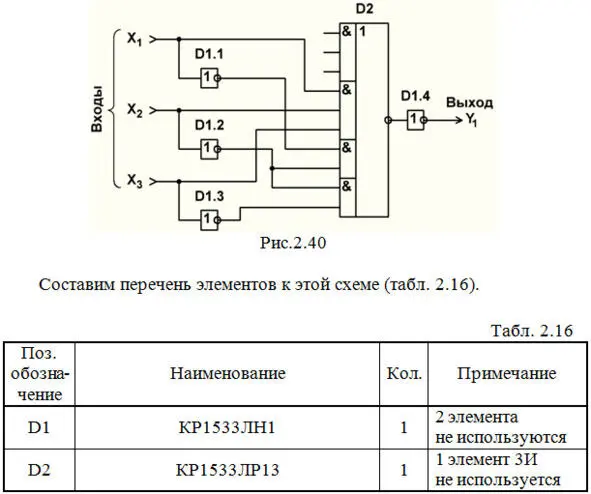
П р и м е ч а н и е: один элемент 3Ииз микросхемы КР1533ЛР13 получается лишним. В схеме рис. 2.40 его входы оставлены свободными , но этого делать нельзя ! В микросхемах ТТЛ и ТТЛШ-структур входы лишних элементов обязательно следует куда-либо подключить , иначе данная ИМС работать не будет (смотрите тему 2.9).