Андрей Павлов - Геометрия - Планиметрия в тезисах и решениях. 9 класс

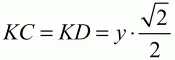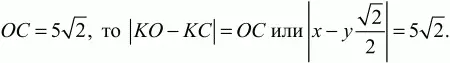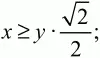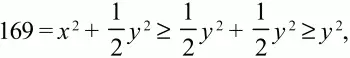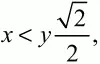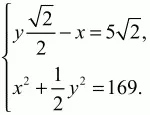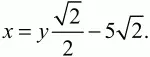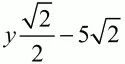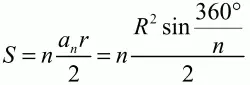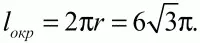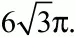
Рис. 161.

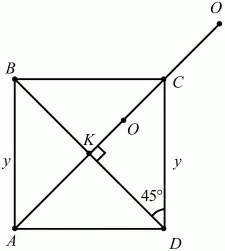
Решение. Так как OB = OD, то точка О лежит на перпендикуляре к середине отрезка BD, т. е. на прямой АС. Обозначим через К точку пересечения диагоналей квадрата. Из условия следует, что ОВ > ОС; значит, точка О лежит по одну сторону с точкой С относительно перпендикуляра к середине отрезка ВС. Отсюда следует, что точка О лежит на луче КС.

Обозначим КО через х и АВ = CD через y. Так как

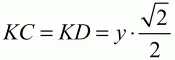
и

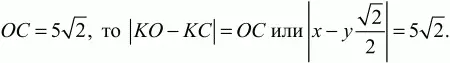
Применяя к прямоугольному треугольнику KOD теорему Пифагора, получаем: OD2= КО2+ KD2или 169 = х2+ 1/2 у2.

Предположим, что КО ? КС или

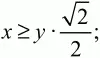
тогда х2 ? 1/2 у2(заметим, что числа x и y неотрицательны) и

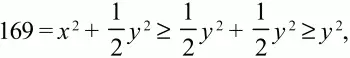
т. е. площадь квадрата не превосходит 169, что противоречит условию. Следовательно,

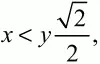
т. е. КО < КС, и точка О лежит внутри квадрата. Теперь получаем

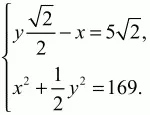
Из первого уравнения

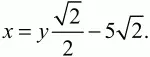
Подставляя

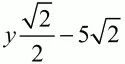
вместо х во второе уравнение, после арифметических преобразований получаем уравнение у2– 10у – 119 = 0. Это квадратное уравнение имеет корни у1 = -7 и у2 = 17. Так как у есть длина отрезка, то у > 0 и, значит, y = 17.

Ответ: длина стороны квадрата равна 17; точка О лежит внутри квадрата.

70. Сторона квадрата равна 7 см. Определите диаметр окружности, описанной около квадрата. (1)

71. В квадрат вписан круг, а в полученный круг вписан квадрат. Найдите отношение площадей квадратов. (1)

72. Квадрат со стороной 3 см срезан по углам так, что образовался правильный восьмиугольник. Найдите сторону восьмиугольника. (2)

73. Дан квадрат ABCD. На его сторонах вовне построены равносторонние треугольники ABM, BCN, CDK, DAL. Найдите площадь четырёхугольника MNKL, если АВ = 1. (2)

Для произвольного выпуклого четырёхугольника S = 1/2 d1d2 sin?. Если в четырёхугольник можно вписать окружность, то суммы его противоположных сторон равны, a S = рr, где р – полупериметр, r – радиус вписанной окружности.

Если около четырёхугольника можно описать окружность, то суммы противоположных углов равны по 180°.

Для правильного n-угольника:

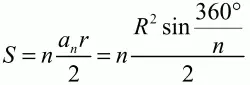
(R и r – радиусы описанной и вписанной окружностей, а – длина стороны правильного n-угольника).

Полезно также помнить, что в правильном шестиугольнике a6 = R.

74. Сторона правильного шестиугольника равна 6. Найдите длину вписанной в него окружности (рис. 162). (1)

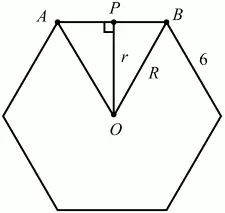
Рис. 162.

Решение. В правильном шестиугольнике сторона равна радиусу описанной окружности. Значит, треугольник АВО – правильный, угол АВО составляет 60°, a OB = R = 6. Радиусы вписанной в правильный шестиугольник окружности перпендикулярны его сторонам. В частности на рис. показано, что r ? АВ, где r = ОР. Тогда из прямоугольного треугольника ОРВ имеем:

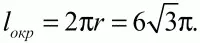
Ответ:

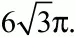
75. Сколько сторон имеет выпуклый многоугольник, у которого все углы равны, если сумма его внешних углов с одним из внутренних равна 468°? (2)

Решение. Сумма внешних углов выпуклого многоугольника равна 360°, сумма внутренних углов равна 180°(n – 2). Величина угла в правильном n-угольнике равна