Андрей Павлов - Геометрия - Планиметрия в тезисах и решениях. 9 класс

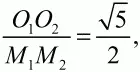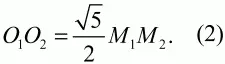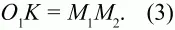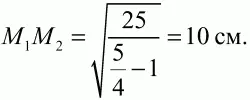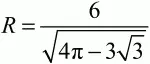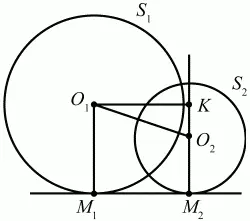
Рис. 167.

Решение. Пусть S1 и S2 – две окружности, удовлетворяющие условию задачи. Поскольку точки М1 и М2 являются точками касания окружностей S1 и S2 с прямой М1М2, то О1М1 ? М1М2 и O2М2 ? М1М2. Соединим центры О1 и O2 этих окружностей и проведём через точку О1 прямую, параллельную прямой М1М2. Пусть точка К будет точкой пересечения прямых O2М2 и прямой, проведённой параллельно прямой М1М2 через точку О1. Получим прямоугольный треугольник O1O2K с гипотенузой O1O2. Применяя к прямоугольному треугольнику О1КO2 теорему Пифагора, имеем:

О1О22= O1K2+ KO22(1)

Поскольку

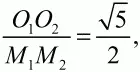
то

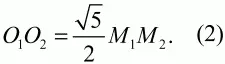
Поскольку КМ2 = О1М1 и КO2 = КМ2 – М2O2, то КO2 = 5 см. Наконец,

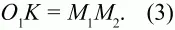
Теперь из равенства (1) с учётом (2) и (3), а также КO2 = 5 см, следует, что 5/4 М1М22= М1М22+ 25, откуда

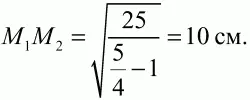
Ответ: 10 см.

85. Дуги А1В1 и А2В2 равной длины 1 принадлежат разным окружностям с радиусами R1 и R2. Найдите отношение градусных мер центральных углов, соответствующих этим дугам. (1)

86. Точка лежит вне круга на расстоянии диаметра от центра круга. Найдите угол между касательными, проведенными из данной точки к данному кругу. (1)

87. В пересечение двух равных кругов вписан ромб с диагоналями 12 и 6 см. Найдите радиус окружностей. (2)

88. В равнобедренный треугольник, у которого боковая сторона равна 10 см, а основание 6 см, вписана окружность. Определите расстояние между точками касания, находящимися на боковых сторонах треугольника. (2)

89. Дано круговое кольцо, площадь которого Q. Определите длину хорды большего круга, касательной к меньшему. (2)

90. Круг радиуса

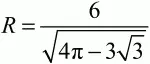
разделен на два сегмента хордой, равной стороне вписанного в этот круг правильного треугольника. Определите площадь меньшего из этих сегментов. (2)

91. Хорды АВ и АС имеют одинаковую длину. Величина образованного ими вписанного в окружность угла равна ?/6. Найти отношение площади той части круга, которая заключена в этом угле, к площади всего круга. (3)

Если в предыдущем параграфе мы рассматривали задачи, в которых центральное место принадлежит формулам планиметрии и тригонометрии, то теперь перейдем к задачам, где главную роль будут играть не формулы, а теоремы о свойствах и признаках геометрических фигур. Задачи в параграфе разбиты уже не по объекту исследования (треугольник, трапеция, круг и т. д.), а по ведущей идее решения.

Если в условии задачи говорится об описанной около треугольника окружности, то в большинстве случаев строить её не нужно. И наоборот, когда речь идёт о вписанной в треугольник окружности. Здесь не только нужно строить саму окружность, но и проводить радиусы к точкам касания (перпендикуляры к сторонам), а также соединять центр окружности с вершинами треугольника. При этом образуются равные треугольники.

92. В прямоугольном треугольнике точка касания вписанной окружности делит гипотенузу на отрезки длиной 5 и 12 см. Найдите катеты треугольника (рис. 168). (1)

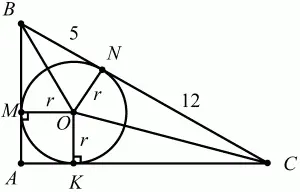
Рис. 168.

Решение. Впишем в треугольник ABC окружность и соединим её центр О с вершинами В, С. Проведём также перпендикуляры ОК, ON, ОМ (см. рис.). Они являются радиусами вписанной в треугольник окружности. Из равенства треугольников ВМО и BNO следует, что ВМ = BN = 5. Аналогично, из равенства треугольников ОКС и ONC следует, что КС = NC = 12. Заметим также, что AMOK– квадрат и, значит, AM = АК = r. Получаем, что АВ = АМ + МВ = r + 5, АС = АК + КС = r + 12. По теореме Пифагора получаем: АВ2+ АС2= ВС2.

(r + 5)2+ (r + 12)2= 172;

r2+ 10r + 25 + r2+ 24r + 144 = 289;

2r2+ 34r – 120 = 0;

r2+ 17r – 60 = 0; r = 3.

Катеты равны 5 + r = 8 и 12 + r = 15.

Ответ: 8 см; 15 см.