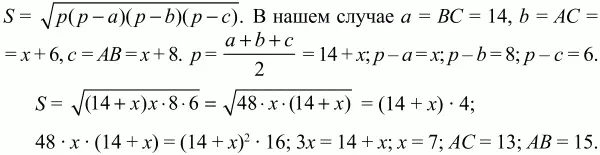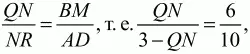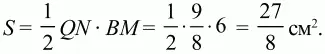Андрей Павлов - Геометрия - Планиметрия в тезисах и решениях. 9 класс

93. В треугольник вписана окружность с радиусом 4. Одна из сторон треугольника разделена точкой касания на отрезки, длины которых 6 и 8. Найдите длины сторон треугольника (рис. 169). (2)

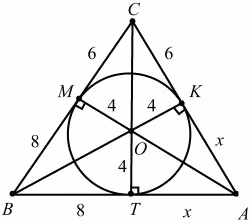
Рис. 169.

Решение. Как и в предыдущей задаче, изобразим вписанную в треугольник окружность и соединим центр окружности О с вершинами треугольника. Проведем также перпендикуляры ОМ, ОТ, ОК, являющиеся радиусами окружности. Получены три пары равных треугольников: OAK и ОAT, ОВМ и ОВТ, ОСМ и ОСК. По условию одна из сторон треугольника разделена точкой касания на отрезки, длины которых 6 и 8. Пусть для определенности эта сторона – ВС и ВМ = 8, МС = 6. Тогда ВТ = ВМ = 8, СК = СМ = 6. Длины отрезков АК и AT обозначим через х. Для нахождения величины х воспользуемся формулой S = рг. По формуле Герона

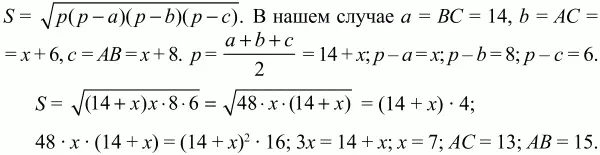
Ответ: 13; 14; 15.

94. Точка касания окружности, вписанной в равнобедренный треугольник, делит боковую сторону на отрезки в 3 и 4 см, считая от основания. Найдите периметр треугольника. (1)

95. Около окружности описана равнобокая трапеция, у которой боковая сторона точкой касания делится на отрезки 4 и 9 см. Найдите площадь трапеции. (2)

96. В прямоугольный треугольник, периметр которого равен 36 см, вписана окружность. Гипотенуза делится точкой касания в отношении 2:3. Найти длины сторон треугольника. (3)

В ряде задач используют свойства параллельных прямых: при пересечении двух параллельных прямых третьей образуются равные углы (рис. 170).

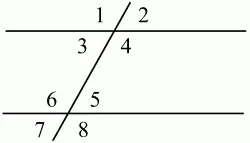
Рис. 170.

Квартеты равных углов:?1 = ?4 = ?6 = ?8; ?2 = ?3 = ?5 = ?7.

Особенно часто эти свойства применяются при решении задач на параллелограмм.

97. В параллелограмме ABCD проведена биссектриса угла А, которая пересекает сторону ВС в точке F. Найдите длину BF, если сторона АВ = 11 (рас. 171). (1)

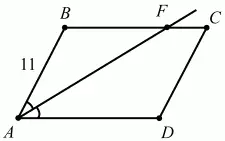
Рис. 171.

Решение. Из рисунка видно, что ?BFA = ?FAD (внутренние накрест лежащие при параллельных прямых), но ?BAF = ?FAD по условию, и поэтому ?BFA = ?BAF. Значит, треугольник ABF – равнобедренный, и BF = АВ = 11.

Ответ: 11.

98. В параллелограмме ABCD сторона АВ равна 6 см, а высота, проведенная к основанию AD, равна 3 см. Биссектриса угла BAD пересекает сторону ВС в точке М так, что МС = 4 см. N – точка пересечения биссектрисы AM и диагонали BD. Вычислить площадь треугольника BNM (рис. 172). (3)

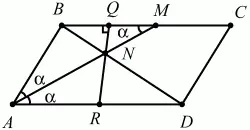
Рис. 172.

Решение. Пусть АВCD – данный в условии задачи параллелограмм. Проведем через точку N высоту параллелограмма QR. Обозначим через ? величину угла ВАМ; тогда величина угла АМВ равна ?, т. к. ВС||AD и AM – секущая. Следовательно, треугольник АВМ равнобедренный и ВМ = АВ = 6 см, откуда заключаем, что ВС = AD = ВМ + МС = 6 + 4 = 10 см. Поскольку ?ВМА = ?MAD и ?MBN = ?BDA, как накрест лежащие углы при параллельных ВС и AD, то треугольники BMN и AND подобны по двум углам. Так как в подобных треугольниках сходственные стороны пропорциональны сходственным высотам, то из подобия треугольников AND и BNM имеем:

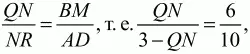
откуда QN = 9/8 см.

Площадь треугольника BNM равна:

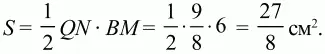
Ответ: 27/8 см2.

99. В параллелограмме ABCD угол BCD равен 60°, длина стороны АВ равна а. Биссектриса угла BCD пересекает сторону AD в точке N. Найдите площадь треугольника NCD. (1)

100. Периметр параллелограмма равен 90 см и острый угол содержит 60°. Диагональ параллелограмма делит его тупой угол в отношении 1:3. Найдите стороны параллелограмма. (1)

101. В параллелограмме ABCD биссектриса тупого угла В пересекает сторону AD в точке F. Найдите периметр параллелограмма, если АВ = 12 и AF: FD = 4:3. (1)

Теорема Фалеса (а также теоремы Чевы и Менелая) применяются в первую очередь тогда, когда в задаче даны соотношения между отрезками. Очень часто при этом приходится проводить дополнительный отрезок. Идеи использования теоремы Фалеса хорошо видны на следующих примерах.