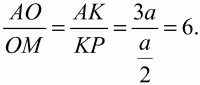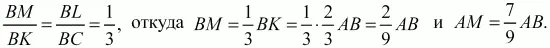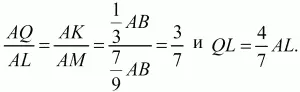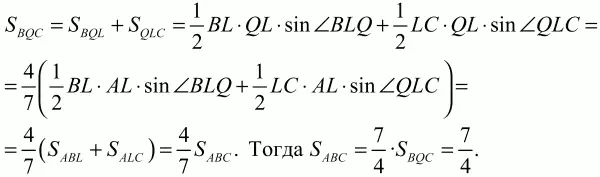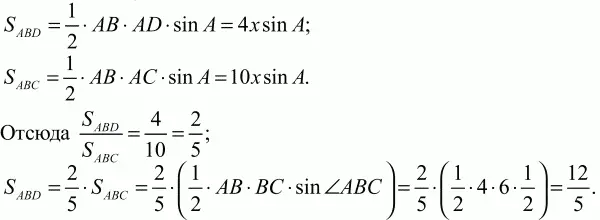Андрей Павлов - Геометрия - Планиметрия в тезисах и решениях. 9 класс

102. Докажите, что медианы в треугольнике делятся в отношении 2:1, считая от вершины (известная теорема школьного курса математики). (2)

Самый простой путь решения (рис. 173):

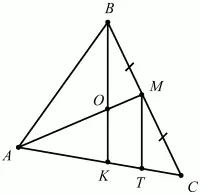
Рис. 173.

Проведем медианы AM и ВК, а также отрезок МТ, параллельный ВК. Имеем: т. к. ВМ = МС, то КТ = ТС. Но тогда АК = КС = 2КТ и, значит, АО: ОМ = АК: КТ = 2, что и требовалось доказать.

103. В треугольнике ABC на стороне ВС взята точка М так, что MB = МС, а на стороне АС взята точка К так, что АК = 3 ? КС. Отрезки ВК и АМ пересекаются в точке О. Найдите AO/OM (рис. 174). (2)

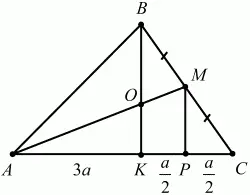
Рис. 174.

Решение. Обозначим длину отрезка КС через а, тогда АК = За. Проведём MP||ВК По теореме Фалеса КР = РС = a/2. По теореме о пропорциональных отрезках имеем:

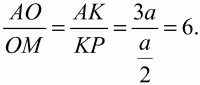
Ответ: 6.

104. В треугольнике ABC на стороне АВ взята точка К так, что АК: ВК = 1:2, а на стороне ВС взята точка L так, что CL: BL = 2:1. Пусть Q – точка пересечения прямых AL и СК. Найти площадь треугольника ABC, если дано, что площадь треугольника BQC равна 1 (рис. 175). (3)

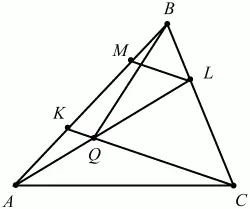
Рис. 175.

Решение. Проведём через точку L прямую LM параллельно прямой СК. Из подобия треугольников MBL и КВС следует, что

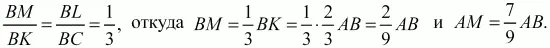
Из подобия треугольников AKQ и AML находим:

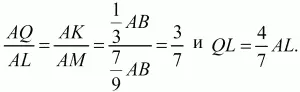
Кроме того, имеем следующие равенства:

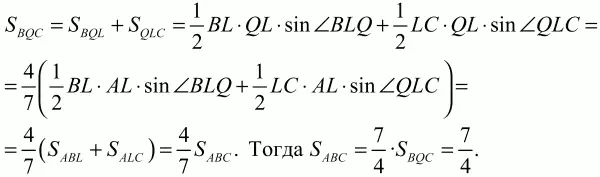
Ответ: 7/4.

105. ВМ: МС = 3:1, АК = КВ. Найдите: SAKO/SABC(рис. 176). (2)

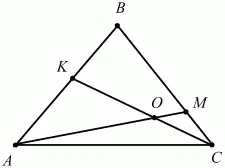
Рис. 176.

106. На сторонах АВ и АС треугольника ABC взяты точки M и N, такие, что AM/MB = CN/NA = 1/2.

Отрезки BN и СМ пересекаются в точке К. Найти отношения отрезков BK/KN и CK/KM.(2)

Биссектриса треугольника обладает одним замечательным свойством: она делит противолежащую сторону на отрезки, пропорциональные соответствующим боковым сторонам (рис. 177).

с/а = d/b или c/d = a/b.

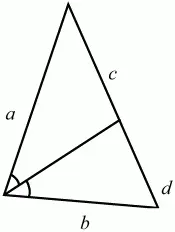
Рис. 177.

Это свойство часто используется в задачах, в которых фигурирует биссектриса треугольника.

107. В треугольнике ABC проведена биссектриса AD. Найдите периметр треугольника ABC, если АС = 4; DC = 2; BD = 3 (рис. 178). (1)

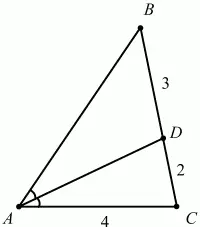
Рис. 178.

Решение. По свойству биссектрисы BD/AB = DC/AC; 3/AB = 2/4; АВ = 6.

Периметр треугольника РАВС = 6 + 5 + 4 = 15.

Ответ: 15.

108. Дан треугольник ABC, в котором ?В = 30°, АВ = 4, ВС = 6. Биссектриса угла В пересекает сторону АС в точке D. Определите площадь треугольника ABD (рис. 179). (2)

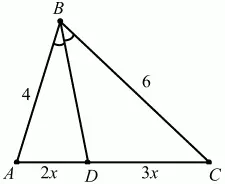
Рис. 179.

Решение. По свойству биссектрисы AD/DC = AB/BC = 4/6 = 2/3.

Пусть AD = 2х; DC = Зх.

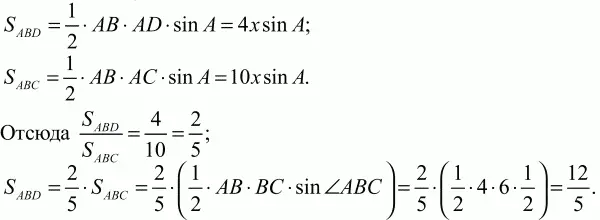
Ответ: 12/5.

109. В треугольнике ABC, где АВ = 6, АС = 4, биссектриса AL и медиана ВМ пересекаются в точке О. Найдите BO/OM (1).

110. Определите стороны треугольника, если медиана и высота, проведённые из вершины одного угла, делят этот угол на три равные части, а сама медиана равна 10 см. (2)

Два треугольника подобны: по двум углам, по двум сторонам и углу между ними, по трём сторонам. Очень важно в задаче увидеть подобные треугольники или другие подобные фигуры. Для этого нужна хорошая практика решения задач.

При решении задач на прямоугольный треугольник полезно знать, что высота, проведённая из прямого угла, делит его на два подобных треугольника (рис. 180):