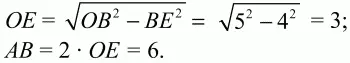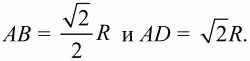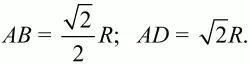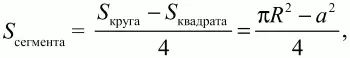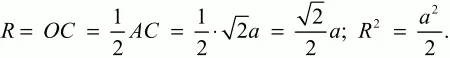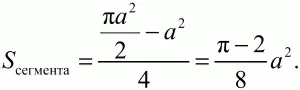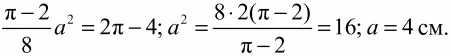1.7. Задачи на прямоугольник
Для прямоугольника справедливы все формулы для параллелограмма, только угол между сторонами равен 90°. Поэтому S = ab = 1/2d2d2 sin?.
Примеры решения задач
61. Прямоугольник вписан в окружность радиуса 5 см. Одна из сторон равна 8 см. Найдите другие стороны прямоугольника (рис. 156). (1)
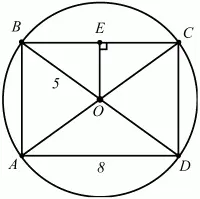
Рис. 156.
Решение. Очевидно, что центр описанной около прямоугольника окружности является точкой пересечения диагоналей прямоугольника. Из рисунка видно, что ОВ = 5, BE = BC/2 = 8/2 = 4.
Тогда по теореме Пифагора находим:
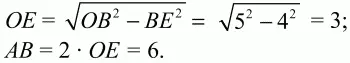
Ответ: 6 см; 8 см; 6 см.
62. Стороны прямоугольника 5 и 4 см. Биссектрисы углов, прилежащих к большей стороне, делят противолежащую сторону на 3 части. Найдите длины этих частей (рис. 157). (2)
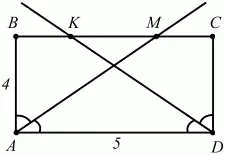
Рис. 157.
Решение. Проведем в прямоугольнике ABCD биссектрисы AM и DK (см. рис. 157). Получим:?ВАМ = 1/2 ?BAD = 1/2 ?90° = 45°. Отсюда следует, что ?АВМ – равнобедренный (?ВMA = 45°) и, значит, ВМ = АВ = 4. МС = ВС – ВМ = 5–4 = 1.
Очевидно, что ВК = МС = 1;
КМ = ВС – ВК – МС = 5–1 – 1 = 3.
Ответ: 1; 3; 1.
63. Из всех прямоугольников, вписанных в полукруг, найти прямоугольник наибольшей площади (рис. 158). (3)
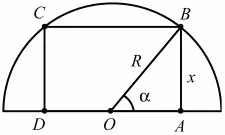
Рис. 158.
Решение. Обозначив ?АОВ =?, получим: АВ = R sin ?, АО = R cos ?, S = AB ? AD = AB ? 2AO = 2R2sin ? ? cos ?, 0° < ? < 90°.
Воспользуемся формулой синуса двойного аргумента и будем иметь:
S = R2sin2?. Так как sin2? ? 1, то S максимальна при условии sin2? = 1, т. е. когда 2? = 90°, ? = 45°. При этом S = R2. Стороны прямоугольника при этом будут равны
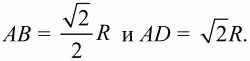
Ответ:
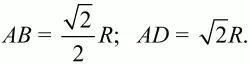
Задачи для самостоятельного решения
64. Диагональ прямоугольника делит угол в отношении 2:1. Найдите отношение сторон прямоугольника. (1)
65. Площадь прямоугольника равна 9?3 см2, а величина одного из углов, образованного диагоналями, равна 120°. Найдите стороны прямоугольника. (2)
66. Площадь прямоугольника ABCD равна 48, а длина диагонали равна 10. На плоскости, в которой расположен прямоугольник, выбрана точка О так, что OB = OD = 13. Найти расстояние от точки О до наиболее удаленной от нее вершины прямоугольника. (3)
Если а – сторона квадрата, d – его диагональ, то S = a2= d2/2.
Примеры решения задач
67. Радиус окружности, в которую вписали квадрат, равен 6. Найдите площадь квадрата (рис. 159). (1)
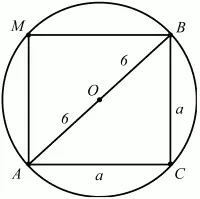
Рис. 159.
Решение. Очевидно, что центр описанной около квадрата окружности есть точка пересечения его диагоналей. Это означает, что ОВ – радиус окружности и ОВ = 6. Тогда АВ = 12 и по теореме Пифагора AC2+ ВС2= AB2. Обозначив длину стороны квадрата через а, получим: а2+ а2= 122; 2 ? а2= 144; а2 = 72. Sквадрата = a2= 72.
Ответ: 72.
68. Сторона квадрата, вписанного в окружность, отсекает сегмент, площадь которого (2? – 4) см2. Найдите периметр квадрата (рис. 160). (2)
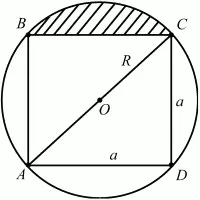
Рис. 160.
Решение. Площадь заштрихованного сегмента, как видно из рисунка, можно вычислить по формуле:
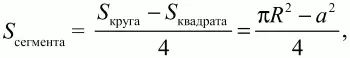
где а – длина стороны квадрата, R – радиус описанной окружности. Выразим R через а.
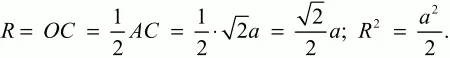
Таким образом,
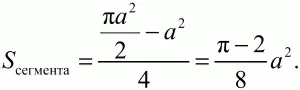
С учётом условия получаем уравнение:
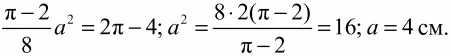
Рквадрата = 4a = 4 ? 4 = 16 см.
Ответ: 16 см.
69. В плоскости дан квадрат с последовательно расположенными вершинами А, В, С, D и точка О. Известно, что OB = OD = 13, ОС = 5?2 и что площадь квадрата больше 225. Найти длину стороны квадрата и выяснить, где расположена точка О – вне или внутри квадрата (рис. 161). (3)
Читать дальше
Конец ознакомительного отрывка
Купить книгу