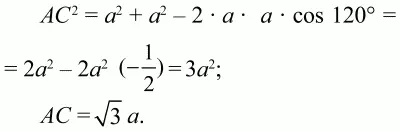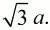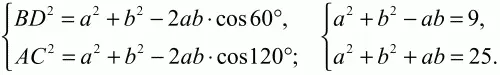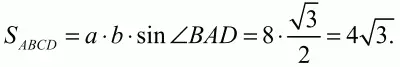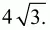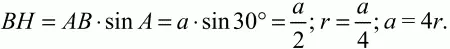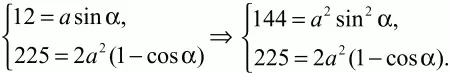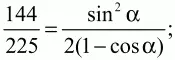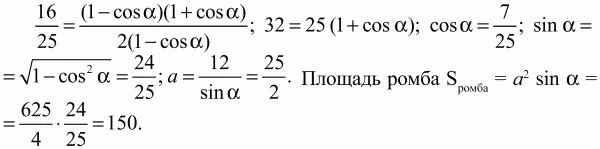Решение. По условию задачи ?А + ?С = 132°. Но, так как в параллелограмме противоположные углы равны, то ?А = ?С = 132°/2 = 66°. Учтём также, что ?А + ?В = ?С + ?D = 180°. Имеем:?В = ?D = 180° – 66° = 114°.
Ответ: 66°, 114°, 66°, 114°.
51. Одна из диагоналей параллелограмма разбивает его на два равносторонних треугольника со стороной а. Найдите длину другой диагонали (рис. 152). (1)
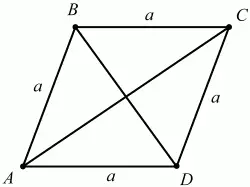
Рис. 152.
Решение. Раз ?ABD и ?BCD – равносторонние, то углы ?BAD = ?BCD = 60°, тогда ?ABC = 120°.
По теореме косинусов из треугольника ABC получаем:
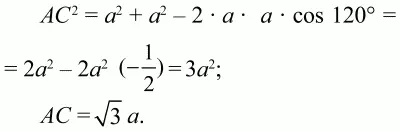
Ответ:
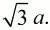
52. Найдите площадь параллелограмма, если его диагонали 3 и 5, а острый угол параллелограмма 60° (рис. 153). (2)
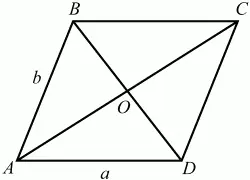
Рис. 153.
Решение. Обозначим стороны параллелограмма: AD = а, АВ = b, ?BAD = 60°. BD = 3; АС = 5. Очевидно, что ?ABC = 120°. По теореме косинусов из треугольников ABD и АСВ имеем:
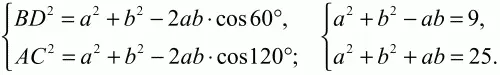
Вычитая первое уравнение из второго, получим 2ab = 16. Тогда площадь будет равна:
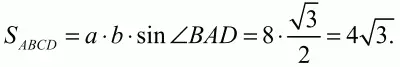
Ответ:
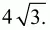
Задачи для самостоятельного решения
53. В параллелограмме с периметром 32 см проведены диагонали. Разность между периметрами двух смежных треугольников равна 8 см. Найдите длины сторон параллелограмма. (1)
54. В параллелограмме ABCD длина диагонали BD, перпендикулярной стороне АВ, равна 6. Длина диагонали АС равна 2?22. Найдите длину стороны AD. (1)
55. Параллелограмм ABCD, у которого АВ = 153, AD = 180, BE = 135 (BE – высота), разделен на три одинаковые по площади фигуры прямыми, перпендикулярными AD. На каком расстоянии от точки А находятся точки пересечения этих перпендикуляров с AD? (2)
Для ромба характерны все формулы для параллелограмма, только а = b.
Примеры решения задач
56. Тупой угол ромба в 5 раз больше его острого угла. Во сколько раз сторона ромба больше радиуса вписанной в него окружности (рис. 154)? (1)
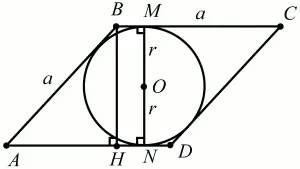
Рис. 154.
Решение. Пусть сторона ромба равна а. В ромбе, как и во всяком параллелограмме, сумма внутренних односторонних углов BAD (обозначим этот угол ?А) и ABC (обозначим его ?В) равна 180°. Получаем систему уравнений:

Радиус r вписанной окружности, как видно из рисунка, равен половине высоты ВН ромба (2r = MN = ВН). Но из ?АВН следует, что
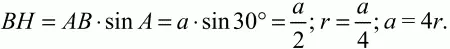
Ответ: в 4 раза.
57. Высота ромба равна 12, а одна из его диагоналей равна 15. Найдите площадь ромба (рис. 155). (2)
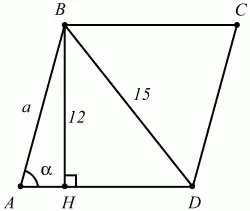
Рис. 155.
Решение. Для нахождения площади ромба нам нужно знать длину стороны ромба и хотя бы один из его углов. Пусть АВ = а; ?А = ?. Проведём высоту ВН. Из ?АВН находим, что ВН = AB ? sin ?; 12 = asin ?. Из ?ABD по теореме косинусов BD2= АВ2+ AD2– 2AB ? AD ? cos ?; 152= а2 + а2– 2 ? a ? acos ?; 225 = 2а2(1 – cos ?). Получаем систему уравнений:
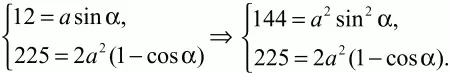
Делим первое уравнение на второе:
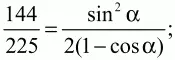
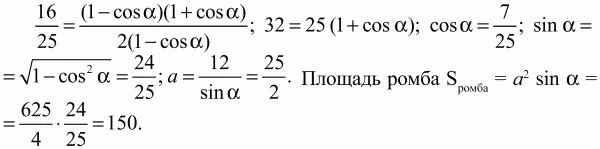
Ответ: 150.
Задачи для самостоятельного решения
58. Диагональ ромба равна его стороне, ее длина 10 см. Найдите вторую диагональ и углы ромба. (1)
59. В ромб, сторона которого 20 см, вписан круг. Найти площадь круга, если одна диагональ ромба больше другой в 4/3 раза. (2)
60. В ромб с острым углом 30° вписан круг, площадь которого равна Q. Найдите площадь ромба. (2)
Читать дальше
Конец ознакомительного отрывка
Купить книгу