Владимир Арнольд - Теория катастроф

Линии второго семейства — гладкие кривые. На кривой К они касаются линий первого семейства. В интересующей нас точке 3 оба семейства касаются линии К. Из этих соображений уже нетрудно усмотреть, что сеть предельных линий вблизи точки 3 выглядит так, как указано на рис. 58: выше кривой К линии второго семейства поднимаются при движении вдоль допустимого направления, ниже — опускаются (выбор направлений линий сети допускает еще несколько вариантов, аналогичных изображенному; разобравшись в рис. 58, читатель легко разберется в них сам).

Теперь на рис. 58 видно, что левее точки 3 граница области достижимости идет по линии второго предельного направления, а правее — первого (горизонтального). В точке 3 обе линии имеют второй порядок касания (как прямая и кубическая парабола). В окрестности этой точки граница достижимости диффеоморфна [6] Диффеоморфизм — это замена координат, гладкая вместе с обратной заменой. графику функции у = х 2| х |.

Таким образом, точки 1 и 2 на рис. 57 и точка 3 на рис. 58 дают примеры устойчиво реализуемых событий на границе области достиэжимости, вызывающих особенности первых трех видов с. 49. Особенности четвертого вида возникают в ситуации рис. 59.

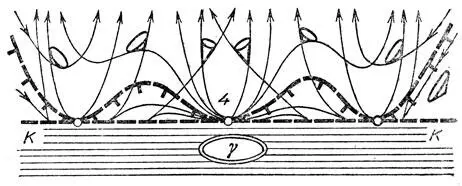
Рис. 59. Сложенные особенности на границе области достижимости

На этом рисунке, как и на рис. 58, цель находится внутри заштрихованной области полной управляемости. На границе К этой области расположены точки плоскости, в которых выпуклая индикатриса проходит через нуль. Ясно, что в управляемых системах общего положения это явление — прохождение индикатрисы через 0 — реализуется на линии. По одну сторону этой линии К лежит область полной управляемости (индикатриса окружает 0), по другую — область с двумя предельными направлениями. На разделяющей их границе К оба эти поля направлений сливаются в одно — поле направлений касательных к индикатрисам в нуле.

В общей точке кривой К направление этого поля составляет с К ненулевой угол. Событие, приводящее к особенности четвертого типа на границе области достижимости, — это касание кривой К с предельным направлением. Для систем общего положения такое касание реализуется в отдельных точках границы области полной управляемости К. На рис. 59 таких точек на кривой К три; средняя из них обозначена цифрой 4.

Чтобы изучить сеть предельных линий в окрестностях этих особых точек, полезно рассмотреть наше двузначное поле предельных направлений как однозначное поле направлений на поверхности, двулистно накрывающей область выше кривой К.

С этой целью рассмотрим множество всех направлений линейных элементов на плоскости. Это множество является трехмерным многообразием, так как направление определяется точкой приложения линейного элемента (две координаты) и еще своим азимутом (одна угловая координата).

Множество всех предельных направлений составляет подмножество множества всех направлений. Это подмножество — гладкая поверхность в трехмерном многообразии всех направлений. Трехмерное многообразие всех направлений проектируется на исходную плоскость (линейный элемент проектируется в свою точку приложения). Поверхность, образованная предельными направлениями, проектируется при этом в часть плоскости, расположенную выше кривой К. Это отображение проектирования поверхности на плоскость над кривой К имеет особенность, а именно складку Уитни.

Двузначное поле предельных направлений на плоскости определяет на построенной поверхности однозначное поле направлений всюду, кроме тех самых особенных точек кривой К (где индикатриса в 0 касается К), которые мы хотим изучать.

Предельные линии обоих полей предельных направлений после перехода на построенную поверхность образуют систему фазовых кривых гладкого векторного поля с особенностями в интересующих нас точках. Эти особые точки могут быть узлами, фокусами или седлами (на рис. 59 средняя точка — узел, а обе крайние — седла). Таким образом, расположение предельных линий на исходной плоскости получается из расположения фазовых кривых векторного поля в окрестности особой точки при отображении складки Уитни. Хотя это отображение Уитни и фазовые кривые не вполне независимы (в частности, над К фазовые кривые касаются ядра проектирования), сказанного достаточно, чтобы исследовать расположение предельных линий вблизи особой точки (между прочим, такую же картину образуют асимптотические линии вблизи параболической кривой на поверхности).