Владимир Арнольд - Теория катастроф

Управляемая система в фазовом пространстве задается так: в каждой точке пространства дан не один вектор скорости (как в обычной эволюционной системе), а целее множество векторов, называемое индикатрисой допустимых скоростей (рис. 54).

Задача управления состоит в том, чтобы, выбирая в каждый момент времени вектор скорости из предосталяемого индикатрисой набора допустимых скоростей, достичь заданной цели (например, прийти за кратчайшее время на заданное подмножество фазового пространства).

Зависимость кратчайшего времени достижения цели от начальной точки может иметь особенности. Рассматривавшиеся в н. 10 особенности функции минимума расстояния до кривой — частный случай (индикатриса — окружность, а цель — кривая). В отличие от этого частного случая особенности кратчайшего времени в общей задаче управления изучены весьма слабо.

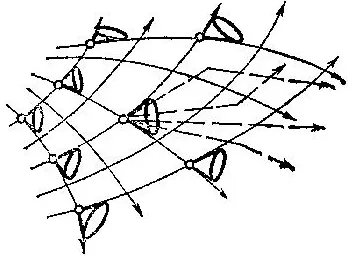
Рис. 54. Поле индикатрис допустимых скоростей управляемой системы

В общем случае достичь цели можно не при любом начальном условии. Точки фазового пространству из которых можно достичь цели (за любое время), называются областью достижимости .

Граница области достижимости может иметь особенности даже в том случае, когда пи цель, ни поле индикатрис в различных точках фазового пространства особенностей не имеют. Мы приводим ниже классификацию особенностей границы достижимости в общей управляемой системе па фазовой плоскости в случае, когда индикатрисы и цель — гладкие кривые (по А. А. Давыдову).

Из четырех типов особенностей границы три записываются простыми формулами (при подходящем выборе локальных координат на плоскости):

1) у = |х|, 2) у = х|х|, 3) у = х 2|х|.

Особенность четвертого тина связана с теорией дифференциальных уравнений, неразрешенных относительно производной, называемых также неявными дифференциальными уравнениями.

Такое уравнение имеет вид F(х, у, р) = 0, где р = dy/dx. Геометрически уравнение F = 0 задает поверхность в трехмерном пространстве с координатами (х, у, р). Она называется поверхностью уравнения .

Условие р = dy/dx выделяет плоскость в каждой точке нашего трехмерного пространства. Эта плоскость состоит из векторов, у-компонента которых в р раз больше х-компоненты, где р — координата точки приложения. Такая плоскость называется контактной. Контактная плоскость в каждой точке вертикальна (содержит направление оси р). Все вместе контактные плоскости задают поле контактных плоскостей, называемое также контактной структурой.

Контактная структура высекает на поверхности уравнения поле направлений (с особыми точками в тех местах, где контактная плоскость касается поверхности). Поверхность уравнения здесь предполагается гладкой. Это условие выполняется для уравнений общего положения.

Вопрос о строении типичных особых точек неявных дифференциальных уравнений рассматривался еще в прошлом веке, и король Швеции Оскар II включил его, наряду с проблемой трех тел, а список из четырех вопросов на премию 1885 г.

Решение этого вопроса было получено лишь в 1985 г. А. А. Давыдовым в виде побочного продукта исследования областей достижимости управляемых систем па плоскости.

Ответ доставляет следующий список нормальных форм (к которым уравнение приводится локальным диффеоморфизмом плоскости):

У = (х + kр) 2.

В зависимости от значения параметра к здесь возможны три случая. Особая точка поля на поверхности уравнения может оказаться седлом, узлом или фокусом. Отображение проектирования поверхности уравнения на плоскость (х, у) вдоль оси р имеет особенностью складку. В окрестности типичной точки складки уравнение приводится к нормальной форме Чибрарио (1932), х = р 2. Все особые точки автоматически попадают на складку. Результат складывания изображен на рис. 55: особые точки па плоскости (х, у) называются сложенным седлом ( узлом, фокусом соответственно). Оказывается, несмотря па сложность узора, образованного интегральными кривыми па плоскости (х, у), он (даже не только топологически, но и с точностью до диффеоморфизма) однозначно определяется единственным "модулем" k (как и фазовый портрет соответствующего векторного поля на плоскости вблизи особой точки).

Сложенные особые точки — седла, узлы, фокусы — встречаются во многих приложениях. Рассмотрим, например, асимптотические линии на поверхности в трехмерном пространство (поверхность имеет с касательными прямыми касание выше первого порядка в каждой своей точке). Для поверхности общего положения сеть асимптотических линий заполняет область гиперболичности, где поверхность имеет отрицательную кривизну (как обыкновенное седло). Через каждую точку области гиперболичности проходят две асимптотические лини и область гиперболичности ограничена линией параболических точек, на которой оба асимптотических направления совпадают.