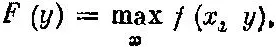Владимир Арнольд - Теория катастроф

Линия критических значений отображения g tназывается его каустикой . Ее можно определить как место пересечений бесконечно близких лучей (траекторий частиц), т. е. так же, как обычную оптическую каустику.

Таким же образом описание метаморфоз оптических каустик доставляет нам описание перестроек скоплений частиц (мест бесконечной плотности среды) при потенциальном движении.

Первая особенность на плоскости выглядит как серпик с полукубически заостренными вершинами (в трехмерном пространстве новорожденная каустика имеет вид блюдца). Я. Б. Зельдович назвал такую каустику блином (первоначально блины интерпретировались как галактики, позже — как скопления).

При дальнейшем движении среды рождаются новые блины. Кроме того, имеющиеся блины начинают перестраиваться и могут взаимодействовать друг с другом. Одна из типичных последовательностей событий в двухмерной среде изображена на рис. 49.

Все возможные в трехмерной среде элементарные перестройки изображены на рис. 44, 45 (получение этих результатов уже требует сложной математической теории лагранжевых особенностей).

В результате перестроек плотность имеет особенности различных порядков на поверхностях блинов, на линиях и в отдельных точках. Будем характеризовать особенность средней плотностью в ε-окрестности рассматриваемой точки (т. е. отношением массы, попавшей к ε-окрестность, к объему окрестности).

Рис. 49. Сценарий взаимодействия 'блинов' Зельдовича

В точках каустики средняя плотность стремится к бесконечности когда радиус окрестности ε стремится к пулю.

Порядок величины средней плотности в различных точках каустик таков:

Каустика ε -1/2

Ребро возврата ε -2/3

Ласточкин хвост ε -3/1

Кошелек, пирамида ε -1

При изменении времени в отдельные моменты появляются особенности А 5со средней плотностью порядка ε -1/5и D 5(ε -1и ε -1).

Согласно астрофизикам, в те времена, когда радиус Вселенной был раз в тысячу меньше нынешнего, крупномасштабное распределение вещества во Вселенной было практически однородным, а поле скоростей — практически потенциальным. Дальнейшее движение частиц привело к образованию каустик, т. е, особенностей плотности и скоплений частиц. До образования блинов плотность остается достаточно малой, чтобы считать среду бесстолкновительной. После этого момента среду можно считать бесстолкновительной, если предполагать что значительная часть массы Вселенной сосредоточена в массивных нейтрино; если же большая часть массы приходится на протоны и нейтроны, то к выводам из геометрии каустик и их перестроек следует относиться с осторожностью, так как среда перестает быть бесстолкновительной.

Выводы о скоплении вещества на поверхностях с преимущественным скоплением вдоль некоторых линий (шнуров), соединяющихся в особых точках (узлах), по-видимому, соответствуют астрономическим наблюдениям, по крайней мере в общих чертах (С. Ф. Шандарин).

Многочисленные особенности, бифуркации и катастрофы (скачки) возникают во всех задачах о нахождении экстремумов (максимумов, минимумов), задачах оптимизации, управления и принятия решений. Представим себе, например, что мы должны выбрать х так, чтобы обеспечить наибольшее значение функции f (х) (рис. 50). При плавном изменении функции оптимальное решение меняется скачком, перескакивая с одного из двух конкурирующих максимумов (Л) на другой (В).

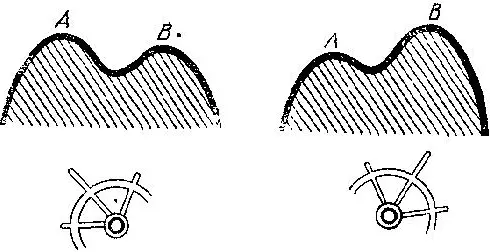
Рис. 50. Разрыв оптимального управления

Ниже мы рассмотрим несколько задач такого рода; все они далеки от полного решения, хотя в некоторых классификация особенностей проведена достаточно далеко.

Рассмотрим семейство f(х, у) функций переменной х, зависящих от параметра у. При каждом фиксированном значении параметра у вычислим максимум функции, обозначим его через

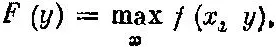
Функция F непрерывна, но не обязательно гладкая, даже если f — многочлен.

Пример 1 . Пусть у — азимут луча зрения, х — дальность, f — угловая высота ландшафта на расстоянии х при азимуте у (рис. 51). Тогда F определяет линию горизонта. Ясно, что линия горизонта гладкой поверхности может иметь изломы и они неустранимы малым шевелением.