Владимир Арнольд - Теория катастроф

Рис. 42. Перестройка плоского сечения поверхности с ребром возврата

Метаморфозу 3 также можно увидеть на видимом контуре, для этого достаточно посмотреть на двугорбого верблюда, проходя мимо него (рис. 43). В момент метаморфозы профиль имеет такую же особенность, как кривая у 3= х 4.

Рис. 43. Перестройка 'верблюд'

Все перестройки видимых контуров поверхностей в общих однопараметрических семействах исчерпываются первыми тремя изображенными на рис. 40, 1 — 3.

Метаморфозы каустик, движущихся в трехмерном пространстве , получаются сечениями больших (трехмерных) каустик в четырехмерном пространстве-времени трехмерными изохронами, Эти метаморфозы изображены на рис. 44 и 45.

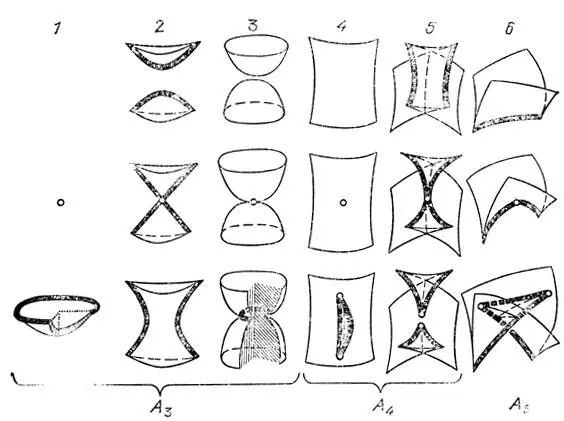
Рис. 44. Типичные переустройки каустик в трехмерном пространстве: серия А

Одна из этих метаморфоз (1) описывает рождение новой каустики "из воздуха". Мы видим, что вновь родившаяся каустика имеет вид блюдца с заостренными краями. Через время t после рождения длина и ширина блюдца порядка √t, глубина порядка t, а толщина порядка t √t.

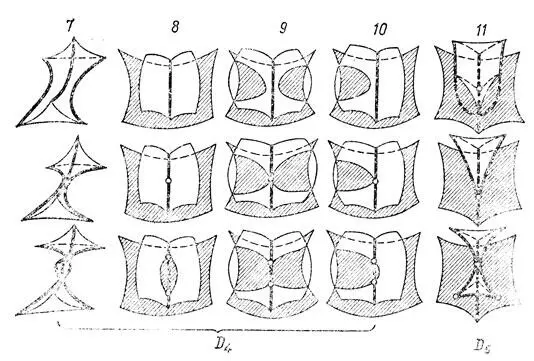
Рис. 45. Типичные перестройки каустик в трехмерном пространстве: серия D

Каустика может сделаться видимой, если на пути светового пучка имеется рассеивающая среда (пыль, туман). В. М, Закалюкин предположил, что каустики этого вида наблюдатели описывают как летающие блюдца.

Ребра возврата движущихся в трехмерном пространстве каустик заметают поверхность бикаустики . Особенности бикаустик общего положения, соответствующих различным метаморфозам рис. 44 и 45, изображены на рис. 46.

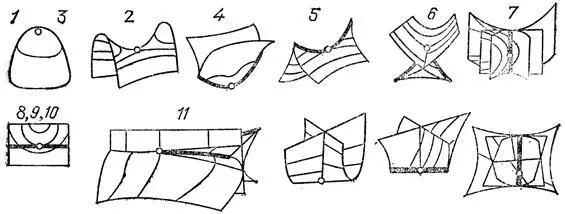
Рис. 46. Типичные особенности бикаустик

Как известно, лучи описывают распространение волн (скажем, световых) лишь в первом приближении; при более точном волновом описании появляется новый существенный параметр — длина волны (лучевое описание пригодно лишь в случае, когда эта длина мала по сравнению с характерным геометрическим размером системы).

Интенсивность света вблизи каустики больше, а вблизи ее особенностей еще больше. Коэффициент усиления оказывается пропорциональным l -α, где l — длина волны, а показатель α — рациональное число, зависящее от характера особенности. Для простейших особенностей значения α таковы:

Каустика 1/6

Ребро возврата 1/4

Ласточкин хвост 3/10

Пирамида 1/3

Кошелек 1/3

Таким образом, ярче всего светятся точечные особенности тина пирамиды и кошелька. В случае движущейся каустики в отдельные моменты времени могут возникать более яркие особенности [4] Все перечисленные особенности классифицируются по типам A k , D k , о которых подробнее рассказано выше. А 5, D 5(см. рис. 44, 45, α = 1/3 для А 5, 3/8 для D 5).

Если свет настолько интенсивен, что способен разрушать среду, то разрушение начнется в точках наибольшей яркости, поэтому показатель α определяет зависимость интенсивности разрушающего среду света от частоты.

Аналогичная описанной выше классификация особенностей каустик и волновых фронтов проведена в многомерных пространствах до размерности 10 (В. М, Закалюкин)

Предсказания теорией особенностей геометрии каустик, фронтов и их перестроек получили полное подтверждение в экспериментах, и сейчас даже кажется странным, почему эта теория не была построена лет двести назад. Дело, однако, в том, что соответствующий математический аппарат не тривиален [5] Первоначальное доказательство теоремы Уитни, о которой мы начали, занимало около 40 страниц; хотя окончательные геометрические результаты теории особенностей легко могут быть понятны и использованы, доказательства продолжают оставаться сложными. и связан с такими разделами математики, как классификации простых алгебр Ли и кристаллографических групп Кокстера, с теорией кос, теорией ветвления интегралов, зависящих от параметров, и т. д — он даже связан (довольно таинственным образом) с классификацией правильных многогранников в трехмерном евклидовом пространстве.