Владимир Арнольд - Теория катастроф

Катастрофисты пытаются избежать серьезной математики. Например, в составленной К. Знманом в 1980 г. обширной библиографии по теории катастроф опущены ссылки на математические работы, вышедшие после 1976 г. Таким образом, катастрофисты продолжают попытки экспериментально нащупать ответы в задачах, давно решенных математиками. Например, в работе 1980 г. о ветровых полях и движении льда можно найти полуудачные попытки угадать список метаморфоз каустик в трехмерном пространстве (см. рис. 44, 45), опубликованный математиками еще в 1976 г.

В настоящее время распределение вещества во Вселенной крайне неоднородно (существуют планеты. Солнце, звезды, галактики, скопления галактик и т. д.). Современная астрофизика считает, что на ранних этапах развития Вселенной таких неоднородностей не было. Как же они образовались? Я. Б. Зельдович в 1970 г. предложил объяснение образования скоплений пылевидной материи, математически эквивалентное анализу возникновения особенностей каустик, начатому в 1963 г. Е. М. Лифшицем, Халатниковым и Судаковым.

Рассмотрим бесстолкновительную среду, т. е. среду настолько разреженную, что ее частицы проходят друг "сквозь" друга, не сталкиваясь. Предположим, для простоты, что частицы не взаимодействуют и движутся по инерции: через время t частица, находившаяся в точке х, перейдет в точку х + vt.

Предположим, что в начальный момент скорость частицы, находящейся в точке х, была v 0(х); векторное поле v 0называется начальным полем скоростей среды . С течением времени частицы будут двигаться и поле скоростей будет меняться (хотя скорость каждой частицы и не меняется, в следующий момент времени эта частица находится на новом месте).

На рис. 47 изображено начальное поле скоростей одномерной среды v 0и получающиеся аз него через время t = 1, 2 и 3 ноля v 1, v 2, v 3. Мы видим, что, начиная с некоторого момента, более быстрые частицы начинают обгонять более медленные; в результате поле скоростей становится трехзначным: через одну точку пространства проходят с разными скоростями три потока частиц.

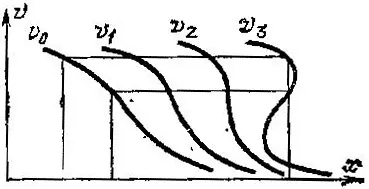
Рис. 47. Эволюция поля скоростей бесстолкновительной среды

Движение нашей среды можно описать как однопараметрическое семейство отображений прямой на прямую . Именно для каждого t определено отображение g t, переводящее начальное положение частицы (х) в конечное: g t= х + v 0(х)t.

Отображение g 0есть тождественное преобразование, оставляющее каждую точку на месте. Отображения, соответствующие моментам t, близким к 0, взаимно однозначны и не имеют особенностей. После момента первого обгона отображение g tимеет две складки.

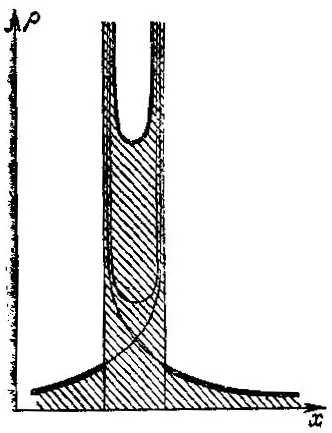
Рис. 48. Особенности плотности после обгона

Пусть в начальный момент плотность среды в точке х была ρ 0(х), С течением времени плотность будет меняться. Нетрудно сообразить, что после обгона график плотности будет иметь вид, изображенный па рис. 48 (на расстоянии 8 от точки складки плотность оказывается порядка 1/√ε).

Таким образом, небольшие отличия начального ноля скоростей от постоянного приводят через достаточно большое время к образованию скоплений частиц (в местах бесконечно большой плотности).

Этот вывод сохраняется при переходе от одномерной среды к среде, заполняющей пространство любой размерности, и при учете влияния на движение ее частиц внешнего силового поля или поля, созданного средой, а также при учете аффектов теории относительности и расширения Вселенной.

Если силовые поля потенциальны (т. е. их работа на любом пути зависит лишь от начала и конца пути) и начальное поле скоростей тоже потенциально, то задача описания особенностей отображений g tи их метаморфоз при изменении t математически тождественна задаче об особенностях каустик и их метаморфоз (то и другое составляет предмет теории так называемых лагранжевых особенностей ).

Точки бесконечной плотности образуют в случае двухмерной среды кривые на плоскости. Эти кривые образованы критическими значениями отображения g t, т. е. его значениями в критических точках (для отображения рис. 1 критические точки — это точки экватора сферы, критические значения — точки видимого контура на горизонтальной плоскости).