Владимир Арнольд - Теория катастроф

В окрестности типичной параболической точки асимптотические линии имеют полу кубическую особенность и вся сеть их приводится к такой же нормальной форме у = с ± х 3/2как и семейство интегральных кривых уравнения Чибрарио.

Однако в окрестности отдельных точек на линии параболичности поведение асимптотических линий сложнее: они устроены как интегральные кривые неявных уравнений вблизи сложенных особых точек (рис. 55).

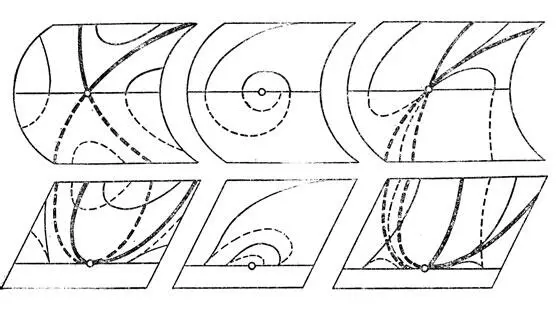
Рис. 55. Сложенные особенности

Сложенные особенности появляются также в теории релаксационных колебаний. Пусть система имеет одну быструю и две медленных переменных, так что полное фазовое пространство трехмерно. Точки, где скорость изменения быстрой переменной равна нулю, образуют (вообще говоря гладкую) поверхность — медленную поверхность системы. Движение фазовой точки состоит из нескольких процессов. Вначале быстрая переменная релаксирует , т. е. фазовая точка быстро движется по "вертикали" (по направлению оси быстрой переменной) к медленной поверхности, затем начинается медленное движение вдоль этой поверхности. Траектории этого движения определяются полем направлений, высекаемым на ней полем плоскостей, натянутых на вертикальное направление (направление оси быстрой переменной) и направление возмущений. Это поле плоскостей определяет, вообще говоря, контактную структуру в фазовом пространстве, и особенности медленного движения описываются, вообще говоря, сложенными особыми точками рис. 55.

В качестве последнего примера тех же особенностей рассмотрим движение материальной точки в потенциальной яме (или у потенциального барьера) в присутствии трения. Обозначим (рис. 56) через х координату точки, а через Е ее полную энергию. Проекции фазовой траектории на плоскость (х, Е) имеют при подходе к графику потенциальной энергии полукубические, вообще говоря, особенности. Минимуму (максимуму) потенциальной энергии отвечает особая точка. Для потенциальной энергии общего положения получаются все те же сложенные особенности Давыдова.

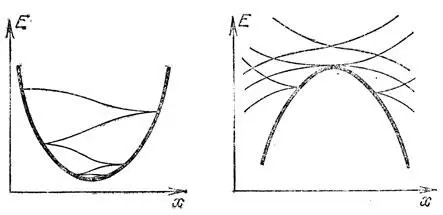
Рис. 56. Диссипация энергии в яме и у барьера

Причина, по которой сложенные особенности встречаются столь часто, состоит в том, что часто встречаются как обычные особенности векторного поля, так и складывания. Неожиданным здесь является лишь то, что комбинирование складывания с особенностью не приводит к большему разнообразию случаев, чем в классификации самих особенностей векторных полей. А именно, рассмотрим складывание как инволюцию (диффеоморфизм, квадрат которого — тождественное преобразование) на плоскости, несущей векторное поле с особой точкой. Если линия неподвижных точек инволюции проходит через особую точку поля и инволюция на этой линии меняет знак каждого вектора поля на противоположный, то такая инволюция (почти всегда) переводится в любую другую инволюцию с такими свойствами при помощи диффеоморфизма, двигающего вдоль себя каждую фазовую кривую заданного поля. Этот (довольно неожиданный) результат является источником всей описанной выше теории.

Четвертая особенность границы достижимости получается из двух сепаратрис сложенных седел, входящих с разных сторон в сложенный узел. Приведенная выше нормальная форма сложенного узла позволяет явно выписать нормальную форму четвертой особенности, но я здесь не буду этого делать.

Примеры управляемых систем и целей, приводящих к указанным особенностям границы достижимости, изображены на рис. 57, 58, 59. На этих рисунках цель у обозначена двойной линией, граница области достижимости — Т-образным пунктиром (ножка буквы Т обращена в сторону области достижимости). Линии со стрелками касаются краев конусов допустимых направлений в каждой точке; горизонтально заштрихована область "полной управляемости, (выпуклая оболочка индикатрисы окружает 0). Рассматривая рис. 57 — 59 читатель может проверить неустранимость особенностей 1 — 4.

Чтобы разобраться в этих рисунках, мы построим сеть предельных линий , определяемую следующим образом.

В каждой точке вне области полной управляемости направления допустимых скоростей расположены внутри угла, меньшего 180°.

Стороны этого угла определяют направления предельных скоростей в данной точке. Таким образом, в каждой точке вне области полной управляемости возникают два предельных направления. Интегральные кривые нолей предельных направлений (т. е. кривые, имеющие предельное направление в каждой своей точке) называются предельными линиями .