Владимир Арнольд - Теория катастроф

На рис. 59 изображен один из вариантов этого расположения. На рисунке видно, что изображенная Т-образным пунктиром граница области достижимости образована проекциями сепаратрис седел (крайних особых точек) при отображении двулистно накрывающей поверхности на плоскость. Над точкой 4 на накрывающей лежит особая точка типа "узел". В этот узел входят с разных сторон две сепаратрисы седел.

В узле эти две кривые имеют общую касательную и (в случав общего положения) могут быть заданы уравнениями парабол степени α > 1 вида

у = А | х | αпри х ≤ 0, у = В | х | αпри х ≥ 0

в подходящей системе координат.

Четвертая особенность границы области достижимости получается из этой пары парабол степени α на накрывающей поверхности при отображении складки Уитни.

Это обстоятельство показывает, между прочим, ошибочность чрезвычайно распространенного среди катастрофистов вульгарного истолкования деклараций Р. Тома о том, что "в природе встречаются только устойчивые явления и потому при изучении каждой задачи следует изучать устойчивые случаи, отбрасывая остальные как нереализуемые". В данном случае особенности первых трех типов устойчивы (с точностью до диффеоморфизмов), а четвертого нет. В то же время все 4 типа особенностей встречаются одинаково часто и изучение последней ничуть не менее важно, чем исследование остальных трех.

Об особенностях области достижимости, функции времени и оптимальной стратегии в управляемых системах общего положения с фазовым пространством большей размерности известно удивительно мало — лишь в 1982 г. доказано, что область достижимости является топологическим многообразием с краем.

Одним из промежуточных вопросов при исследовании управляемых систем оказывается вопрос об особенностях выпуклых оболочек гладких многообразий (кривых, поверхностей,...).

Выпуклой оболочкой множества называется пересечение всех содержащих его полупространств. Индикатриса управляемой системы может быть невыпуклой.

Однако оказывается, что невыпуклую индикатрису можно заменить ее выпуклой оболочкой.

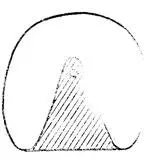
Рис. 60. Овыкупление индикатрисы при помощи смешанной стратегии

Например, индикатриса скоростей яхты при встречном ветре невыпукла (рис. 60). Против ветра можно, однако, двигаться галсами , применяя смешанную стратегию , т. е. перемежая участки движения с разными скоростями, принадлежащими индикатрисе. Средняя скорость движения при смешанной стратегии принадлежит множеству средних арифметических используемых векторов индикатрисы, т. е. выпуклой оболочке.

Особенности выпуклых оболочек кривых и поверхностей общего положения в трехмерном пространстве исследованы В. Д. Седых и В. М. Закалюкиным. В случае кривых с точностью до гладкой замены переменных оболочка задается в окрестности каждой своей точки одной из шести формул:

z ≥ 0, z ≥ | x |, z ≥ x | x |,

z ≥ min (u 4+ хu 2+ уu), z ≥ min 2(х, у, 0),

{z ≥ min 2(х, у, 0), х + у ≥ 0}

(рис. 61). В случае поверхностей — одной из трех формул

z ≥ 0, z ≥ х | х |, z ≥ ρ 2(х, у),

где ρ (х, у) — расстояние от точки (х, у) до угла у ≥ с | х | (рис. 62). Число с > 0 является модулем (инвариантом): оболочки, соответствующие разным с, не сводятся одна к другой гладким преобразованием.

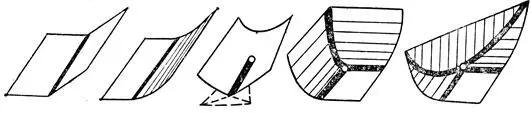
Рис. 61. Типичные особенности выпуклых оболочек пространственных кривых

Особенности выпуклых оболочек в пространстве большей размерности мало изучены. Согласно В. Д. Седых, выпуклая оболочка общего k-мерного многообразия в пространстве размерности выше к+2 имеет модули, являющиеся функциями к переменных.

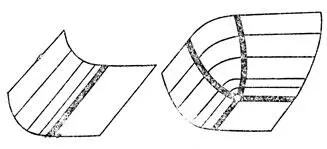
Рис. 62. Типичные особенности выпуклых оболочек поверхностей

Тень, отбрасываемая бесконечно-гладким или даже аналитическим выпуклым телом, может, как это ни кажется странным, иметь особенности. А именно, граница тени трехмерного выпуклого тела может иметь разрывы третьей производной, а тела размерности 4 и выше — даже второй (И. А. Богаевский, 1990).

Много новых интересных особенностей возникает в оптимизационных задачах с ограничениями, например в задаче об обходе препятствия. Их исследование привело к новым результатам в одной из самых классических областей математики — геометрии гладких поверхностей в трехмерном пространстве.