Владимир Арнольд - Теория катастроф

Гладкая кривая на плоскости может иметь касательную со сколь угодно большим числом точек касания (рис. 63), но это не в случае общего положения. Малым шевелением кривой можно добиться того, что никакая прямая не будет касаться ее более чем в двух точках.

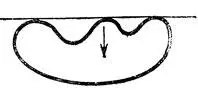
Рис. 63. Тройная касательная нетипичной кривой

В скольких точках может касаться прямой поверхность общего положения? Немного подумав или поэкспериментировав, читатель может убедиться, что наибольшее число точек касания равно четырем ; сохраняя три точки касания, прямую можно двигать, две — двигать в двух направлениях.

Порядок касания прямой с кривой или поверхностью также может быть различным (например, порядок касания оси х с графиком у = х 2первый, х 3— второй и т. д.) Плоская кривая общего положения не имеет касательных выше второго порядка (второй порядок касания встречается в отдельных точках кривой, называемых точками перегиба ).

Для поверхности в пространстве дело обстоит уже не так просто. В точках, близ которых поверхность не выпукла, имеются касательные выше первого порядка (они называются асимптотическими касательными ). Для поверхности общего положения касательные третьего порядка имеются на некоторой линии, а четвертого — в отдельных точках; касательных выше четвертого порядка общая поверхность не имеет.

Все точки поверхности общего положения делятся по порядкам касательных на следующие 7 классов (рис. 64):

1) область эллиптических точек (все касательные порядка 1);

2) область гиперболических точек (две асимптотические касательные).

Эти две области разделяет общая граница:

3) линия параболических точек (одна асимптотическая касательная).

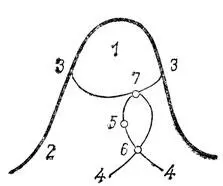
Рис. 64. Классификация точек на гладкой поверхности

Внутри области гиперболичности выделяется особая линия:

4) кривая перегиба асимптотических линий (есть касательная третьего порядка).

Наконец, на этой кривой выделены еще особые точки трех типов:

5) точка двойного перегиба касательная четвертого порядка;

6) перегиб обеих асимптотических линий (две касательные третьего порядка);

7) обилие точки линий 3) и 4).

Для поверхностей общего положения в точках 6) происходит пересечение двух ветвей линии перегибов под ненулевым углом, а в точках 7) — касание (первого порядка) линий 3) и 4).

Описанная классификация точек поверхности (О. А. Платонова, Е. Е. Ландис) следующим образом связана с классификацией особенностей волновых фронтов.

Математики называют точками объекты любой природы. Рассмотрим, например, множество всех невертикальных прямых на плоскости (х, у).

Такие прямые задаются уравнениями вида у = ах + b. Следовательно, одна прямая определяется парой чисел (а, b) и может рассматриваться как точка плоскости с координатами (а, b). Эта плоскость называется двойственной к исходной плоскости . Ее точки — это прямые исходной плоскости.

Если на исходной плоскости дана гладкая кривая, то в каждой ее точке имеется касательная прямая. При движении точки вдоль кривой касательная меняется, следовательно, движется точка двойственной плоскости. Таким образом, на двойственной плоскости возникает кривая — множество всех касательных исходной кривой. Эта кривая называется двойственной к исходной .

Если исходная кривая гладкая и выпуклая, то двойственная кривая тоже гладкая, если же исходная кривая имеет точку перегиба, то на двойственной кривой ей соответствует точка возврата (рис, 65).

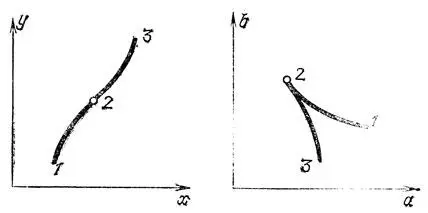
Рис. 65. Двойственность точек перегиба и возврата

Кривые, двойственные к гладким кривым общего положения, имеют такие же особенности, как волновые фронты общего положения на плоскости, и так же перестраиваются при общей гладкой деформации исходной кривой, как перестраивается распространяющийся общим образом по плоскости общий фронт.

Точно так же плоскости в трехмерном пространстве образуют двойственное трехмерное пространство , и все касательные плоскости к гладкой поверхности образуют двойственную поверхность . Особенности поверхности, двойственной к поверхности общего положения, такие же, как у волнового фронта, т. е. ребра возврата с ласточкиными хвостами.