Владимир Арнольд - Теория катастроф

Линии параболических точек исходной поверхности соответствует на двойственной поверхности ребро возврата. Особые точки на этой линии (где она касается линии перегиба асимптотических) соответствуют ласточкиным хвостам. Линия самопересечения ласточкиного хвоста состоит из двойных касательных плоскостей исходной поверхности. Следовательно, в точке 7) сливаются две точки касания плоскости с исходной поверхностью, чем и заканчивается однопараметрическое семейство двойных касательных плоскостей.

Классы точек на поверхности общего положения проявляются также в виде различных особенностей видимого контура. Если направление проектирования — общего положения, то особенности — лишь складки и сборки, по теореме Уитни. Однако, выбрав направление проектирования специальным образом, можно получить и некоторые не общие проекции поверхности общего положения. Оказывается, все такие проектирования локально приводятся к проектированиям перечисленных ниже 9 поверхностей z = f (х, у) вдоль оси х: (поверхности проектируются на плоскость, (у, z), приведение осуществляется заменой X (х, у, z), Y (у, z), Z (y, z)).

1 / х 2

2 / х 3+ ху

3 /, 4 х 3± ху 2

5 / х 3+ ху 3

6 / х 4+ ху

7 / х 4+ х 2у + ху 2

8, 9 / х 5+ х 3у ± ху

Видимые контуры, соответствующие этим проекциям, изображены на рис. 66.

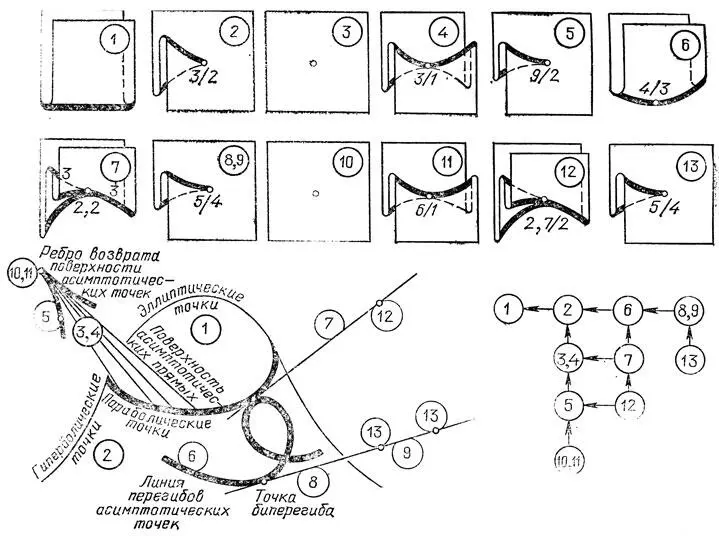
Рис. 66. Видимые контуры и порядки их особенностей для типичных проектирований

Соответствие между классификацией проектирований и точек на поверхности состоит в следующем. 1 — это проектирование по неасимптотическому направлению (складка Уитни).

Проектирование по асимптотическому направлению в общей точке гиперболической области принадлежит типу 2. Это проектирование имеет особенностью сборку Уитни. При малом шевелении направления проектирования особая точка лишь немного перемещается по поверхности: новое направление оказывается асимптотическим в близкой точке. Таким образом, чтобы увидеть сборку, достаточно взглянуть на общую поверхность по асимптотическому направлению .

При движении поверхности или наблюдателя в отдельные моменты появятся особенности 3, 4 и 6.

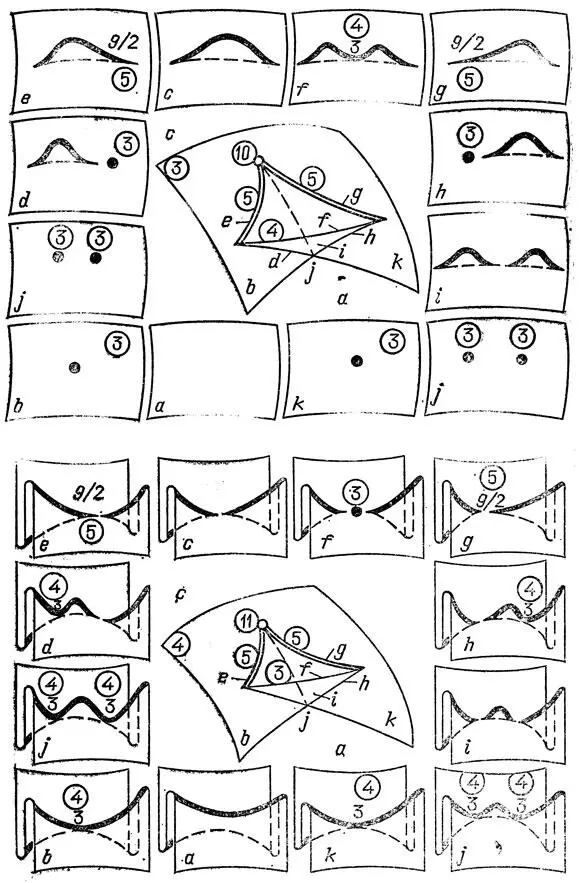
Рис. 67. Бифуркации проектирований при деформации центра проекции: случаи 10 — 11, z = х 3± ху 4

Проектирования 6 (и 8 или 9) соответствуют гиперболической области (а именно асимптотическим касательным третьего и четвертого порядков соответственно).

По спине двугорбого верблюда (см. рис. 43) проходит линия перегиба асимптотических. Касательные третьего порядка, приложенные в ее точках, образуют поверхность. Проходя мимо верблюда, мы дважды пересекаем эту поверхность. В момент пересечения видимый контур спины имеет особенность тина у 3= х 4, а проектирование — тип 6.

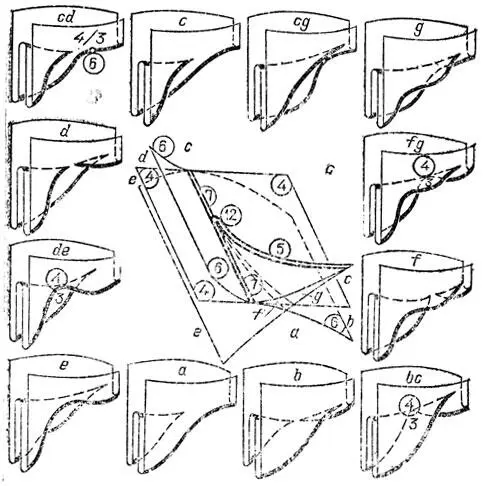
Рис. 68. Бифуркации проектирований: случай 12, z = х 4+ х 2у + ху 3

Остальные особенности возникают при проектировании по направлению, асимптотическому в параболической точке. Простейшие из них — особенности 3 и 4. Проектирование 3 реализуется в момент, когда мы, спускаясь с бугра, начинаем видеть его контур (см. рис. 41). Первая появляющаяся точка контура — параболическая.

При прохождении особенности 4 происходит слияние или разделение двух компонент видимого контура.

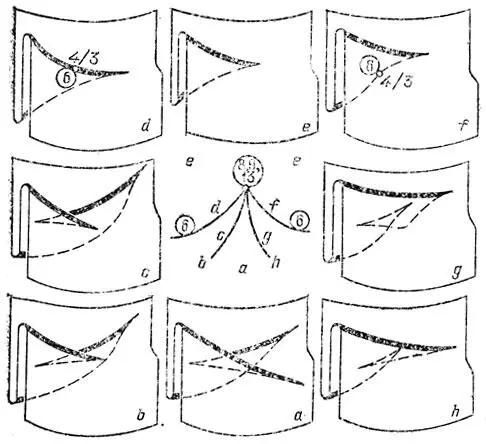
Рис. 69. Бифуркации проектирований: случай 13, z = х 5+ ху

Особенности 5, 7, 8 и 9 реализуются лишь при изолированных направлениях проектирования, и их нужно специально искать. (8 и 9 — проектирование вдоль касательной четвертого порядка, 7 — вдоль параболической касательной третьего порядка, 5 — точка "параллельности асимптотических в бесконечно близких параболических точках"). При проектированиях из отдельных точек реализуются еще 4 особенности 10 — 13: z = х 3± ху 4, z = х 4+ х 2у + ху 3, z = х 5+ ху (рис. 66 — 69).

Рассмотрим в трехмерном евклидовом пространстве препятствие, ограниченное гладкой поверхностью (рис. 70). Ясно, что кратчайший путь из х в у в обход препятствия состоит из отрезков прямых и отрезков геодезических (кратчайших линий) на поверхности препятствия. На геометрию кратчайших путей сильно влияют х различные перегибы поверхности препятствия.