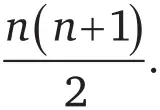Хаим Шапира - Восемь этюдов о бесконечности. Математическое приключение

А это подводит нас к третьему уровню: только если понять, почему нечто происходит, – например разложив камни квадратом, – можно исключить всякую возможность ошибки.

Скажи мне – и я забуду. Научи меня – и я запомню. Дай мне сделать – и я пойму.

Подход Пифагора нравится мне тем, что он дает знание третьего рода. Я понимаю, почему выражения верны, на более глубоком уровне. Я не могу проверить все бесконечное количество случаев применения формулы, но, если я получу глубокое понимание происходящего, я пойму, почему эта формула истинна.

Однажды мне попалась в библиотеке книга русского математика Якова Успенского (1883–1947) под названием «Теория уравнений» (Theory of Equations, 1948). Он работал в Стэнфордском университете под именем Джеймс Успенский. Успенский доказал множество разнообразных формул тем же путем, каким доказывал Пифагор, – то есть при помощи иллюстраций.

Начну с весьма простого примера.

Если сложить все числа от 1 до n , результат будет равен

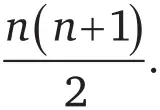
Следующий чертеж объясняет, почему эта формула действует для случая n = 4.

Сумма чисел от 1 до 4 равна половине площади прямоугольника; другими словами, ½ × 4 × 5 = 10.

Ну хорошо, для n = 4 все просто. А что происходит с более крупными числами?

Существует хитрый способ вычисления суммы последовательных чисел от 1 до, скажем, 100. Этот способ тесно связан с историей, главный герой которой – маленький мальчик. Разные страны и народы спорят о том, кто именно был этим мальчиком. Русские утверждают, что это был математик Николай Лобачевский, «Коперник геометрии», и было ему тогда семь лет. Евреи говорят, что это был Барух Спиноза, но возраст называют такой же. Немцы называют героем этого повествования выдающегося математика – на самом деле одного из величайших во всей истории математики – К. Ф. Гаусса (в честь которого, что неудивительно, названа колоколообразная кривая – гауссиана) в шестилетнем возрасте. Немало и таких родителей, которые утверждают, что это произошло с их собственным ребенком.

Поскольку мы только что познакомились на страницах этой книги со Спинозой, я выберу его.

Так вот, однажды маленький Барух сидел на уроке и очень, очень скучал. Но беда была не только в том, что ему было скучно, а еще и в том, что из-за этого он шалил и мешал учителю вести урок. Учитель решил дать мальчику какую-нибудь задачу, которая займет его на долгое время, и велел Баруху сложить все числа от 1 до 100. «Этого ему хватит по меньшей мере до конца урока», – решил учитель.

Но его ожиданиям не суждено было сбыться. Не успел учитель повернуться к доске, как Барух сказал: «Учитель, ответ – 5050».

Мы можем предположить, что Барух еще не был знаком с приведенной выше формулой (он был слишком мал). Как же ему удалось так быстро сосчитать эту сумму?

1 + 2 + 3 + 4 + … + 98 + 99 + 100 =?

Ответ оказывается очень простым и к тому же очень изящным. Барух не стал складывать все числа по порядку: он заметил, что можно сложить первое число с последним (1 + 100 = 101), второе – с предпоследним (2 + 99 = 101), третье – с третьим с конца (3 + 98 = 101) и так далее, вплоть до 50 + 51 = 101, и получить пятьдесят пар, сумма членов каждой из которых равна 101. После этого ему оставалось только умножить 50 на 101, а это очень легко сделать: 50 × 100 = 5000 плюс еще один раз 50, итого 5050.

Умно́, не правда ли? Если подумать об этом несколько секунд, можно понять, что метод маленького Баруха аналогичен Пифагоровой идее раскладывания камешков.

Привычка Пифагора преподавать с использованием камешков также объясняет, почему мы называем некоторые числа «квадратными», «треугольными», «кубическими» и так далее. Он просто давал этим числам названия, соответствующие их геометрическим представлениям.

Например, как можно видеть из иллюстрации, числа 1, 4, 9, 16, 25… – «квадратные»:

Числа 1, 3, 6, 10, 15… – «треугольные»:

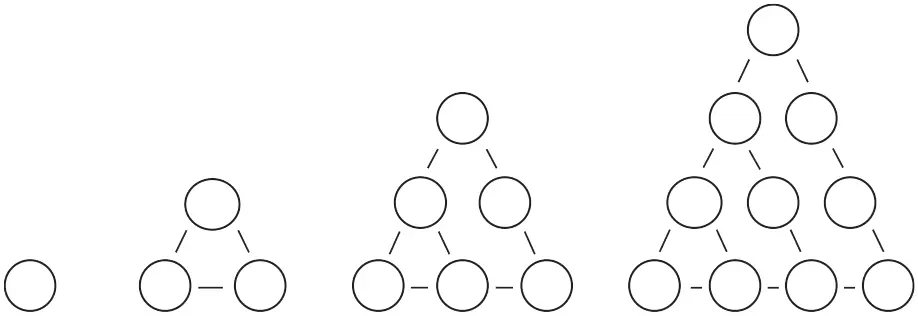
А числа 1, 5, 12… – пятиугольные.

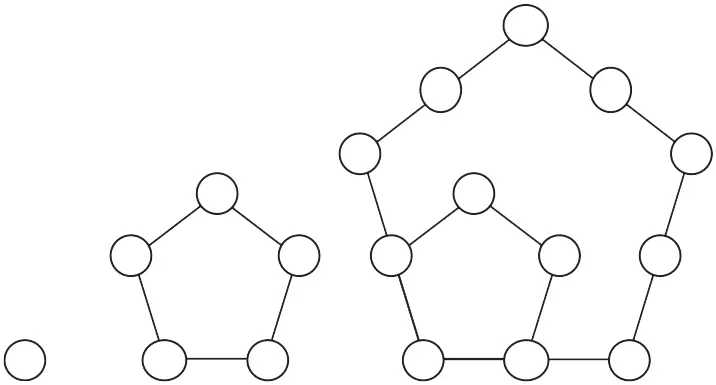
Вернемся к треугольным числам.