Хаим Шапира - Восемь этюдов о бесконечности. Математическое приключение

Математическая индукция – это совершенно поразительный инструмент для доказательства утверждений. Что особенно замечательно, он позволяет получить доказательство для бесконечного множества элементов исходя из доказательства для конечного их числа. Я приведу пример, объясняющий, как работает индукция. Предположим, мы хотим доказать, что следующее равенство справедливо для всех натуральных чисел:

1 + 3 + … + (2 n – 3) + (2 n – 1) = n ².

Доказательство состоит из двух частей. В первой части мы доказываем справедливость так называемого индукционного перехода , то есть несколько странного утверждения, которое гласит: «Если это равенство истинно для n , то оно истинно и для n + 1».

Во второй части нужно доказать так называемую базу индукции , то есть убедиться, что это равенство истинно для n = 1.

Вот и всё! Этим мы доказываем справедливость этого утверждения для всех натуральных чисел.

Все это может показаться сомнительным, но позвольте мне объяснить. Представьте себе, что доказательство для n – это костяшка домино. Если вы когда-нибудь выстраивали ряд костяшек домино, вы знаете, что их ставят так, что, когда некая определенная костяшка падает, она толкает соседнюю, та толкает следующую и так далее – пока не упадут все костяшки. В доказательстве по индукции мы точно так же выстраиваем свои «утверждения» в ряд: если мы доказали утверждение для любого элемента n , это «толкает» утверждение для элемента n + 1. Но, как и в случае костяшек домино, чтобы запустить цепную реакцию падения, нужно подтолкнуть первую костяшку – или, если использовать терминологию математической индукции, доказать базу индукции. Итак, мы совершаем индукционный переход – то есть предполагаем, что истинно следующее равенство:

1 + 3 + … + (2 n – 3) + (2 n – 1) = n ².

Теперь докажем, что оно справедливо и для n + 1, рассуждая следующим образом.

Левая часть равенства имеет вид:

1 + 3 + … + (2( n + 1) – 3) + (2( n + 1) – 1) = 1 + 3 + … + (2 n – 1) + (2 n + 1).

В правой же части должно быть ( n + 1)². Поскольку мы предполагаем, что наше равенство выполняется для n , мы можем утверждать, что:

1 + 3 + … + (2 n – 1) + (2 n + 1) = n ² + (2 n + 1) = ( n + 1)².

Этим завершается доказательство гипотезы индукции. Осталось только толкнуть первую костяшку. Для базы индукции, то есть при n = 1, утверждение, несомненно, справедливо, так как 1 = 1².

Теперь костяшки доказательства начинают падать одна за другой: утверждение для n = 2 вытекает из утверждения для n = 1, утверждение для n = 3 – из утверждения для n = 2 и так далее.

Однако Пифагор придумал способ получше этого. Тот же закон становится совершенно очевидным, если расположить камешки определенным образом.

Один шарик и три шарика легко расставить в форме квадрата размером 2 × 2 клетки:

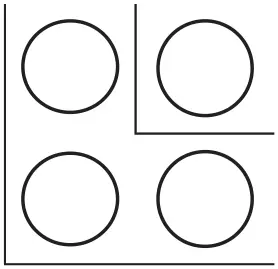
Один шарик, три шарика и еще пять шариков дают правильный квадрат размером 3 × 3:

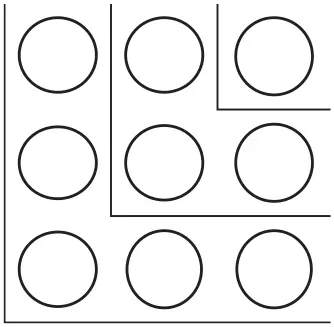
Если же добавить к ним следующее нечетное число, 7, точно так же получится квадрат размером 4 × 4 клетки:

Великий еврейский философ Барух Спиноза различал три вида знания:

1. Вера.

2. Исследование (экспериментирование).

3. Понимание.

Я объясню, о чем идет речь. Если вы сообщаете мне что-то – например что сумма последовательности нечетных чисел равна полному квадрату, – я могу поверить, что вы знаете, о чем говорите. Это первый уровень знания. Однако вполне может быть, что то, что вы мне рассказали, неверно.

Если я не поленюсь проверить эту информацию – то есть рассмотрю несколько примеров и смогу убедиться, что для них это правило выполняется, – я перейду на второй уровень знания. На нем утверждение несколько более достоверно, потому что я видел, что оно действительно справедливо в некоторых случаях, но считать его абсолютно истинным нельзя. Профессор Бено Арбель (1939–2013) показал мне однажды замечательный пример, в котором многократные проверки не позволяют убедиться в истинности утверждения, даже когда их число необычайно велико. Возьмем выражение 991 n ² + 1. Существует ли такое значение n , при котором это выражение дает полный квадрат? Можно подставить множество разных значений n , а потом перебрать кучу других значений n , и все время будет казаться, что это выражение никогда не дает полного квадрата. Но это не так, потому что при n = 12 055 735 790 331 359 447 442 238 767 получается именно полный квадрат! Даже если мы проживем миллиард лет и потратим все это время на подстановки и вычисления, вряд ли мы обнаружим это число.