Rudolf Taschner - Die Zahl, die aus der Kälte kam - Wenn Mathematik zum Abenteuer wird

Abb. 3: Der Erdschatten berandet bei einer Mondfinsternis den Vollmond so, dass seine Größe der einer 75 cm vom Auge entfernt gehaltenen Ein-Euro-Münze entspricht. Hieraus kann man grob den Abstand der Erde vom Mond schätzen.

Kennt man den Abstand des Mondes von der Erde, lässt sich – so glaubte es wenigstens der noch vor Eratosthenes lebende Astronom Aristarch – sogar der Abstand der Sonne von der Erde bestimmen. Sieht man nämlich am Tageshimmel den genauen Halbmond, braucht man, so Aristarchs Idee, nur den Winkel zu messen, der sich zwischen dem Sehstrahl vom Auge zur Sonne und dem Sehstrahl vom Auge zum Mond erstreckt. Denn bei Halbmond ist auf dem Mond der Winkel zwischen dem Sehstrahl vom Auge zum Mond und dem Sonnenstrahl auf den Mond ein exakter rechter Winkel. Kennt man die Winkel des Dreiecks mit Erde, Mond und Sonne als Ecken, weiß man, welche Form das Dreieck besitzt. Und kennt man zusätzlich eine Seite dieses Dreiecks – in unserem Fall: die Länge der Strecke von der Erde zum Mond –, dann kennt man auch die beiden anderen Dreieckseiten.

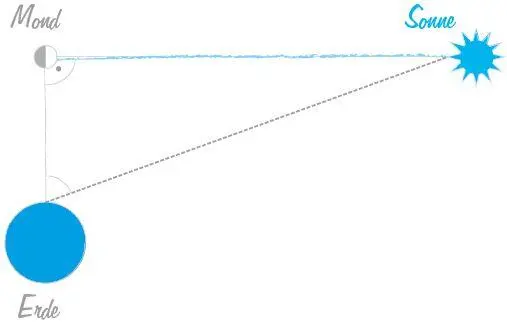
Abb. 4: Prinzip der Abstandsmessung der Erde von der Sonne nach Aristarch: Bei genauem Halbmond schließen der Sehstrahl des Auges von der Erde zum Mond und der Strahl der Sonne zum Mond einen rechten Winkel ein. Wenn man den Winkel zwischen dem Sehstrahl von der Erde zum Mond und dem Sehstrahl von der Erde zur Sonne misst, kennt man die Figur des dabei gebildeten rechtwinkligen Dreiecks. Aus ihr kann man entnehmen, um wie viel weiter die Sonne von der Erde entfernt ist als der Mond. Allerdings ist der zu messende Winkel so nahe dem rechten Winkel, dass Aristarch kein valides Resultat erhalten konnte.

Theoretisch ist das Verfahren des Aristarch einwandfrei. Doch will man es praktisch verwerten, erweist es sich als undurchführbar. Der zu messende Winkel, der sich zwischen dem Sehstrahl vom Auge zur Sonne und dem Sehstrahl vom Auge zum Mond erstreckt, ist fast ein rechter Winkel. Für Aristarch war der Unterschied zu einem exakten rechten Winkel unmessbar klein. Der Sonnenstrahl auf den Halbmond und der Sehstrahl vom Auge zur Sonne sind fast parallel. Die Sonne ist daher um ein beträchtliches Vielfaches weiter von der Erde entfernt als der Mond: 19-mal so weit, schätzte Aristarch. Doch mit dieser Schätzung lag er weit daneben: Die Sonne ist etwa 400-mal weiter von der Erde entfernt als der Mond.

Ungefähr 150 Millionen Kilometer beträgt dieser Abstand. 150 Millionen spricht sich leicht aus, aber die mit dieser Zahl verbundene Distanz unserer Vorstellung zugänglich zu machen, gelingt nicht. Was will das schon besagen, dass man die Erde 3750-mal umrunden müsste, um diese Distanz nur einmal bewältigt zu haben? Oder dass das Licht, das in einer Sekunde 300 000 Kilometer zurücklegt, von der Sonne bis zu uns acht Minuten lang unterwegs ist? All das stimmt, aber übersteigt trotzdem unsere Vorstellungskraft.

Mit dem Abstand von der Erde zur Sonne fangen die astronomischen Distanzen aber erst an. Die uns am nächsten kommenden Sterne sind über 250 000-mal weiter von uns entfernt als die Sonne. Das sind rund 40 Billionen Kilometer. Neuneinhalb Billionen Kilometer legt das Licht innerhalb eines Jahres zurück, auch dies eine unvorstellbare Distanz, die mit dem Wort „ein Lichtjahr“ niedlich abgekürzt wird. Es ist eine Abkürzung, die dringend benötigt wird. Denn die Milchstraße, jene Sterneninsel, in der unsere Sonne als ein durchschnittlicher unter Hunderten Milliarden Sternen enthalten ist, besitzt einen Durchmesser von mehr als 100 000 Lichtjahren. Die nächste ungefähr gleich große Sterneninsel ist der Andromedanebel. Über zwei Millionen Lichtjahre ist er von uns entfernt, aber bei einer sternenklaren Nacht als diffus leuchtender Punkt gerade noch mit bloßem Auge erkennbar. In Kilometer umgerechnet sind zwei Millionen Lichtjahre mehr als 18 Trillionen Kilometer. Eine Zahl, die an die Zahl der Reiskörner erinnert, die der weise Mann vom Maharadscha verlangte.

Doch das ist erst der Anfang, wenn ein Kosmologe über die Größe des Weltalls spricht. Denn Sterneninseln wie die Milchstraße oder der Andromedanebel gibt es zuhauf, wohl mehr als 100 Milliarden. Mit riesigen Teleskopen auf der Erde und mit großen Fernrohren, die in Satelliten eingebaut sind, werden sie in den Tiefen des Alls wahrgenommen. Fast 50 Milliarden Lichtjahre weit kann man theoretisch mit diesen Geräten in die Ferne dringen, danach beginnt der „Ereignishorizont“ des Universums, hinter den, vertraut man Einsteins Allgemeiner Relativitätstheorie, kein Auge und kein Messgerät zu blicken vermag. Rechnet man die 50 Milliarden Lichtjahre in Kilometer um, ergibt dies mehr als 450 Trilliarden Kilometer.

Aussprechen kann man das leicht. Vorstellen kann man es sich nicht.

Die riesigen Dimensionen des Kosmos verleiteten Archimedes dazu, die, wie er meinte, größte Zahl, die es auf Erden gibt, zu berechnen. Denn Archimedes war der Ansicht, dass es vielleicht nicht sinnlos, wohl aber nutzlos sei, von größeren Zahlen zu sprechen als jener, die sich als Antwort auf die Frage ergibt, wie viele der allerkleinsten Teile der Welt im ganzen Universum Platz finden.

Die allerkleinsten Teile der Welt, das sind, so schreibt Archimedes, die Sandkörner. Dabei sollte man eher von einem Staubkorn sprechen, das er sich gedacht hat, denn er geht von folgendem Gedanken aus: Ein Mohnkorn umfasst nicht mehr als zehntausend Sandkörner. Und 25 Mohnkörner aneinandergereiht ergeben die Breite eines Fingers. Doch um ganz sicherzugehen, machte Archimedes das Mohnkorn so klein, dass 40 Mohnkörner aneinandergereiht nur eine einen Zentimeter lange Strecke ergeben. Stellt man sich das kleine Mohnkorn als einen Würfel mit einer Kantenlänge von einem Viertel Millimeter vor, besitzt dieser Würfel ein Volumen von rund 0,016 Kubikmillimetern. Archimedes machte es sogar noch kleiner: 0,01 Kubikmillimeter sollte es bloß groß sein. Zehntausend Sandkörner enthält dieses Korn. Darum hat das Sandkorn, der nach Archimedes allerkleinste Teil der Welt, ein Volumen von mickrigen 0,000001 Kubikmillimetern. Mit anderen Worten: In einen Kubikmillimeter passen eine Million Sandkörner.

Die größte Zahl des Universums ist nun die Sandzahl . Die Zahl der Sandkörner, die im Universum Platz finden.

Den Durchmesser des Kosmos schätzte Archimedes sehr großzügig ab, wobei er sich auf die – wie wir bereits wissen falschen – Daten des Aristarch über den Abstand der Erde von der Sonne berief. Nach Aristarchs Meinung ist die Sonne mehr als 19-mal weiter von der Erde entfernt als der Mond. Der von Aristarch vermutete Abstand zur Sonne ist also, aufgerundet, der Mondabstand von 400 000 Kilometern mal zwanzig: Das macht acht Millionen Kilometer. Sicher passt das Universum, so vermutete Archimedes, in einen Würfel, dessen Kante eine Million mal größer als der Abstand der Erde von der Sonne ist. Das wäre eine Kante mit acht Billionen Kilometer Länge. Noch größer ist ein Würfel, der zehn Billionen Kilometer als Kantenlänge hat. Von diesem ging Archimedes aus. Sein Volumen beträgt eine Sextilliarde Kubikkilometer, also 1039 Kubikkilometer, das bedeutet nach der Ziffer 1 folgen 39 Nullen.

In einen Kubikmillimeter passen eine Million, also 106 Sandkörner. Und weil eine Milliarde Kubikmillimeter, also 109 Kubikmillimeter, in einen Kubikmeter und genauso eine Milliarde Kubikmeter, also 109 Kubikmeter, in einen Kubikkilometer passen, lautet die Sandzahl des Archimedes 106 × 109 × 109 × 1039. Das ist 1063, in Worten: eine Dezilliarde.